How is the classical twin paradox resolved?

Question

I read a lot about the classical twin paradox recently. What confuses me is that some authors claim that it can be resolved within SRT, others say that you need GRT. Now, what is true (and why)?

Answer 1

To understand this paradox it's best to forget about everything you know (even from SR) because all of that just causes confusion and start with just a few simple concepts.

First of them is that the space-time carries a metric that tells you how to measure distance and time. In the case of SR this metric is extremely simple and it's possible to introduce simple $x$, $t$ coordinates (I'll work in 1+1 and $c = 1$) in which space-time interval looks like this

$$ ds^2 = -dt^2 + dx^2$$

Let's see how this works on this simple doodle I put together

The vertical direction is time-like and the horizontal is space-like. E.g. the blue line has "length" $ds_1^2 = -20^2 = -400$ in the square units of the picture (note the minus sign that corresponds to time-like direction) and each of the red lines has length zero (they represent the trajectories of light).

The length of the green line is $ds_2^2 = -20^2 + 10^2 = -300$. To compute proper times along those trajectories you can use $d\tau^2 = -ds^2$. We can see that the trip will take the green twin shorter proper time than the blue twin. In other words, green twin will be younger.

More generally, any kind of curved path you might imagine between top and bottom will take shorter time than the blue path. This is because time-like geodesics (which are just upward pointing straight lines in Minkowski space) between two points maximize the proper time. Essentially this can be seen to arise because any deviation from the straight line will induce unnecessary space-like contributions to the space-time interval.

You can see that there was no paradox because we treated the problem as what is really was: computation of proper-time of the general trajectories. Note that this is the only way to approach this kind of problems in GR. In SR that are other approaches because of its homogeneity and flatness and if done carefully, lead to the same results. It's just that people often aren't careful enough and that is what leads to paradoxes. So in my opinion, it's useful to take the lesson from GR here and forget about all those ad-hoc SR calculations.

Just to give you a taste what a SR calculation might look like: because of globally nice coordinates, people are tempted to describe also distant phenomena (which doesn't really make sense, physics is always only local). So the blue twin might decide to compute the age of the green twin. This will work nicely because it is in the inertial frame of reference, so it'll arrive at the same result we did.

But the green twin will come to strange conclusions. Both straight lines of its trajectory will work just fine and if it weren't for the turn, the blue twin would need to be younger from the green twin's viewpoint too. So the green twin has to conclude that the fact that blue twin was in a strong gravitational field (which is equivalent to the acceleration that makes green twin turn) makes it older. This gives a mathematically correct result (if computed carefully), but of course, physically it's a complete nonsense. You just can't expect that your local acceleration has any effect on a distant observer. The point that has to be taken here (and that GR makes clear only too well) is that you should never try to talk about distant objects.

Answer 2

The "paradox" in the twin paradox is that a naive view of the problem would suggest that the situation ought to be perfectly symmetric: each twin should believe that he or she is really at rest, while the other twin is the one who moves off at high speed then returns. This is incorrect, though, because one of the two necessarily accelerates, which provides a means of distinguishing between the two frames of reference.

You can understand the difference in times entirely from within special relativity, with no need to invoke general relativity. You can easily Google up a dozen different explanations of how it works, but the best I've seen is probably the one in Tatsu Takeuchi's An Illustrated Guide to Relativity. Sadly, being illustrated and not online, it's a bit beyond my ability to reproduce here, but it's worth a look.

The problem that needs to be resolved is that both twins should see the other's clock running slow during the trip, but somehow, the moving twin has to end up seeing less time pass than the Earthbound twin. The resolution is, very roughly, that in the moving frame of the twin on the return trip, the departure point is much farther in the past, so the trip has been going on for a longer time. An observer who has always been in that frame (say the captain of the interstellar transport the twin is hitching a ride on) would say that the Earth clock has always been slow, but it's been going for far longer than the twin's internal clock would suggest.

The details are somewhat subtle, though, which is why there are dozens of semi-contradictory explanations available via Google. It's important to note, though, that it is not the case that the acceleration causes the difference between the clocks (in which case you might actually need GR to work it out). It's the transitions between frames of reference that leads to the difference, not the acceleration itself, and you can get a twin-paradox-like difference between clocks even when both twins undergo exactly the same acceleration, as shown in this American Journal of Physics paper.

Answer 3

You don't need to invoke GR to explain the twin paradox- you only need GR when effects associated with the curvature of space-time need to be taken into account.

The twin paradox simply reflects a fact about the geometry of flat space-time, namely that the elapsed time along a straight path between two events is always longer than the elapsed time along any other path. In the classic twin paradox, one twin follows a straight path between the start and the end, while the other twin doesn't- as a result, the first twin experiences a longer elapsed time.

Answer 4

Carlo Rovelli gives an intuitive account of why only SRT is needed in his new book "The order of time":

‘In motion’ in relation to what? How can we determine which of the two objects moves, if the motion is only relative? This is an issue that has confused many. The correct answer (rarely given) is this: in motion relative to the only reference in which the point in space where the two clocks separate is the same point in space where they get back together. There is only a single straight line between two events in spacetime, from A to B: it’s the one along which time is maximum, and the speed relative to this line is the one that slows time. If the clocks separate and are not brought together again, there is no point asking which one is fast and which one is slow. If they come together, they can be compared, and the speed of each one becomes a well-defined notion.

Answer 5

This answer provides a variation of @Marek's answer that tries to address
@vonjd's concern about the non-inertial observer (in green)
trying to be considered "inertial" (instead of the blue inertial observer).

First, as others have already said, general relativity is not needed to analyze this problem. Special relativity capable of analyzing the situation.

---

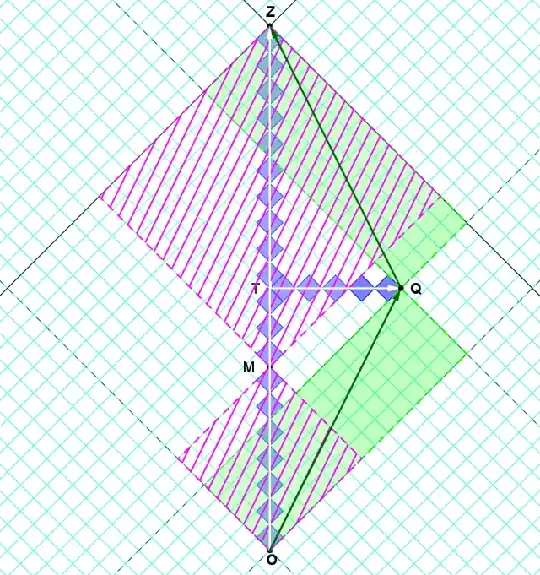
I'll draw a spacetime diagram on rotated graph paper so that we can more easily compute the interval between events.

The causal diamond of OZ is the intersection of the causal future of O and the causal past of Z. The timelike diagonal OZ has length equal to the square-root of the area in units of the grid, whose diamonds are modeled after light-signals traced out by a light-clock at rest in this frame.

Let's verify @Marek's calculation.

By counting, and using the $(+,-)$-signature,

• the area of diamond OZ is (20)(20)=400. So, the timelike diagonal OZ has size 20.
• the area of diamond OQ is (15)(5)=75, and similarly for QZ.
  So, the piecewise-inertial worldline OQZ has length $2\sqrt{75}\approx 17.32$.

One might argue that $OTZ$ is also piecewise-inertial.
So, what makes $OTZ$ inertial and $OQZ$ not inertial?

• Kinematically, $OTZ$ is inertial because $O$, $T$, and $Z$ are collinear and they satisfy: $\sqrt{AreaOZ}=\sqrt{AreaOT}+\sqrt{AreaTZ}=\sqrt{100}+\sqrt{100}=\sqrt{400}$.
• In fact, for any event along $OZ$, e.g., event $M$: we have
  $\sqrt{AreaOZ}=\sqrt{AreaOM}+\sqrt{AreaMZ}=\sqrt{49}+\sqrt{169}=\sqrt{400}$).
• However, for $OQZ$, we have $\sqrt{AreaOQ}+\sqrt{AreaQZ}=\sqrt{75}+\sqrt{75}\neq \sqrt{400}$.
  So, $OQZ$ is noninertial.

Note that no Lorentz transformation can change these results.

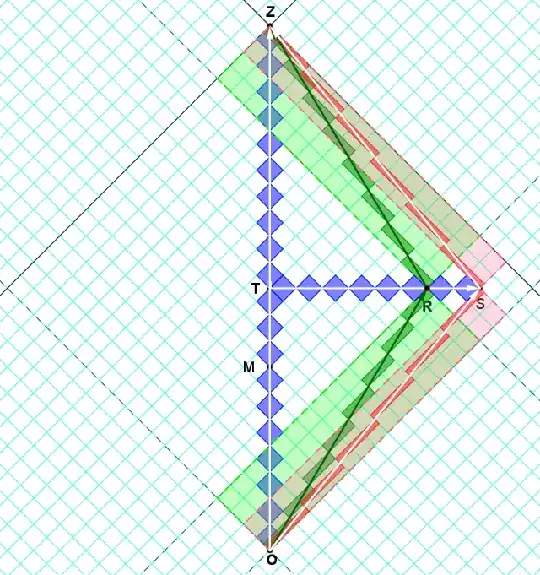
Since $v_{OQ}=\frac{1}{2}$, its doppler factor $k=\sqrt{\frac{1+v}{1-v}}=\sqrt{\frac{3}{2}}$ isn't rational and so the ticks along the diagonal are not easy to draw.

Using instead $v_{OR}=\frac{3}{5}$, or $v_{OS}=\frac{4}{5}$, which have rational doppler factors ($k=2$ and $k=3$, respectively), we can more easily draw and count the ticks along their diagonals.
These diamonds are traced out by their respective light-clocks.

Note that the area of the light-clock diamonds are invariant, indeed because the boost transformation has determinant 1.
Furthermore, Rational $k$'s are associated with Pythagorean triples.

---

For related argument, see my answers for
Equivalence of two definitions of proper time in special relativity
https://physics.stackexchange.com/questions/553682/twins-paradox-why-is-one-frame-considered-to-be-the-accelerating-frame
https://physics.stackexchange.com/questions/242043/what-is-the-proper-way-to-explain-the-twin-paradox

In the end, the lesson of the Twin Paradox is that
"Being able-to-be-at-rest"≠ "Being inertial".

---

For more on this approach, refer to my article
"Relativity on rotated graph paper"
American Journal of Physics 84, 344 (2016);
https://doi.org/10.1119/1.4943251
(early draft at : https://arxiv.org/abs/1111.7254 )

Answer 6

The question is: what do you mean by "classical"? To me the Classical Twin Paradox is what Einstein called the Clock Paradox, i.e. the version without any accelerations. And this paradox has never been resolved.

If there are no accelerations involved in the situation, than the whole paradox results only from the simple equation for time dilatation:

$$ \Delta t' = \frac {\Delta t} {\sqrt{1 - \frac{v^2}{c^2}}} $$

As we can see, there is just constant $v$ there, and yet one of the clocks must be time-dilated.

If someone says that space-travel requires acceleration of a spaceship, they are absolutely right. The thing is that any time-dilatation due to acceleration is only on top of dilatation due to constant $v$.

We can imagine simply that both twins go on a space trip in different spaceships and travel in opposite directions. In such case we can easily assume that they both undergo exactly the same accelerations which effectively "cancel" each other out. And yet we still have the paradox resulting from time dilatation between inertial frames. The above equation still holds. Therefore, we need to answer the question: Which of the twins is younger and why?

As you can see, introducing accelerations only masks the real paradox, and not solves it. And perhaps that's why nobody solves the paradox with real numbers. Because if you make actual calculations, you will immediately see that you need to add time-dilatation due to acceleration to time-dilatation due to constant $v$. Which leaves the other one still unresolved.

In order to illustrate the classical paradox best, we can formulate it in two ways:

1) If one of the twins actually becomes older due to difference in constant $v$, than the axiom of Special Relativity that there are no preferred (inertial) reference frames is falsified. Because this means the reference frame with slower clock is moving with respect to the other in absolute terms. Therefore movement is absolute.

Someone can reply to this that I don't understand SR which allows us to revert the whole situation, i.e. switch the moving and the stationary frames. Sure, but then we have paradox 2):

2) If we claim that clock A is slower than clock B, and also that clock B is slower than clock A, than Special Relativity cannot be proved to be true. For in such case both clocks are late with respect to each other, which boils down to no real time-dilatation at all. If there is a difference measured, however, then we are back to paradox 1), i.e. one of the frames is clearly preferred, and therefore we proved absolute movement exists.

To sum up. There is no solution to the classical (strictly inertial) Twin Paradox. And also, any accelerations do not solve the paradox either - they only mask it.

EDIT: Professor Chad Orzel in his answer gave this paper as a source claiming that dilatation in SR (without accelerations) can be proved. That's simply astonishing, as anybody can see that this paper is based on a trick whereby the parents of the traveling twins stay on Earth and see there is some distance between them equal $γx_0$. However: 1) length calculations in SR are made from the two reference frames, and not from a 3rd one, 2) if twins travel in opposite directions (as in my thought experiment above) you can always claim the other twin is younger, and - most importantly - 3) this paper shows dilatation based on velocity $v$, and yet there is no velocity difference between the twins - they travel in two rockets in the same direction, having been accelerated in exactly the same way. The velocity $v$ is measured from their parents frame, i.e. Earth, and the author even admits that saying that effective velocity between the twins is null. Now how come a paper claiming SR time dilatation between reference frames stationary wrt. each other (and not accelerated) has been accepted for publication?!?! And how come it has been presented here as source by a professor?!

(And if vonjd didn't find this free paper, we might think that some smart guy proved the unprovable. And if I paid for it, I would be simply coned.)

NOTiCE: Any comments concerning this line of reasoning are more than welcome.

Answer 7

The problem is the symmetry break caused by the traveling twin when he changes his direction. This break makes the two twins distinguishable from each other. Before the traveling one changes his direction, both think of their partner to be the younger one (because the time in your own system is always the fastest possible time). So IMHO this paradox has not much to do with general relativity - special relativity can of course not describe accelerated movements, but what really matters is that the twin reverses, not how he accelerates and so on.

Answer 8

Its easy to resolve from the person on earth - he took the doppler effect out of the equation during his observations of the space ship and observed that the clock on the rocket ship was running slow, and confirmed this when the ship arrived back in port, by comparing the two clocks.

The observation according to the traveller is somewhat of a mystery. The traveller looks back at earth, removes the doppler effects and apparently views the earth time running slowly. Without taking his eye of the two clocks, at some point the doppler effect removed time on earth must speed up and overtake that of the travellers clock. When does this happen? - isn't this in contradiction to what we are taught is observed?