How the problem is addressed in literature
The idea that the flow of heat between bodies at very small temperature difference is reversible is a basis of reversibility of Carnot's engine, and therefore, in a sense, a basis of the second principle and of the whole thermodynamics. We can observe that Maxwell and other pioneers of thermodynamics had recognized the importance of the problem: in [MAXWELL] it is stated
The peculiarity of Carnot's engine is, that whether it is receiving heat from the hot body, or giving out to the cold body, the temperature of the substance in the engine differs extremely little from that of the body in thermal communication with it. [...] we may make the actual difference of temperature which causes the flow of heat to take place as small as we please. [...] by working the engine sufficiently slowly these differences may be reduced within any limits we please to assign, so that for theoretical purposes we may regard Carnot's engine as strictly reversible.
However, the ultimate conclusion is not substantiated: the fact that small temperature gradients ensure reversibility of heat flows is taken for granted by Maxwell without proof. On the other hand, in later classic thermodynamics textbooks, such as [PLANCK] and [FERMI], this intriguing matter does not seem to be contemplated. In some modern textbooks, the issue is occasionally mentioned, but in my view, it has not been addressed satisfactorily; this answer intends to delve into this matter more deeply, aiming to provide a more complete and satisfactory examination.
I will cite three excellent books.
a) In [FEYNMAN] it is said that two bodies with infinitesimal difference of temperature can experience reversible heat flows. However, the concept is argued rather vaguely, and a proof is lacking.
b) In [MORAN-SHAPIRO] two bodies at different temperature, able to communicate thermally, are considered. It is said that with a finite temperature difference between them the spontaneous heat transfer would be a source of irreversibility, but the importance of this irreversibility would diminish as the temperature difference approaches zero. Sometimes the absence of a proof, replaced by the sentence "it might be expected", might be acceptable. But in this case the problem is that it is not clear what guarantees that a process that can be carried out with heat flows between bodies at infinitely close temperatures is, in this limit, reversible.
c) Similarly, in [STEANE] two bodies in perfect thermal contact and infinitesimal temperature difference are considered. The author underlines that a change in the circumstances by just more than $\delta T$ will reverse the direction of the heat flow. I think that, although this conclusion is evident, it is not clear why the process must be reversible in the technical sense introduced a few lines earlier in the text: "A reversible process is one such that the system can be restored to its initial state without any net change in the rest of universe".
In brief, I find in the literature an absence of a clear explanation of the link between the "restoring universe" definition of reversible process, and the reversibility of heat flows between bodies with almost the same temperature. However this link is important because it demonstrates that the concept of Carnot's engine, reversible by definition, is meaningful. Reversibility is commonly implicitly assumed to be correct, although it has not formally proven. In the following sections I will demonstrate how, with a simple thought experiment, the gap can be satisfactorily bridged.
Description of thought experiment
Let's consider a body $\xi$ at temperature $T_i$ and let's suppose we want heat it to a temperature $T_f>T_i$ and then to cool it to the initial temperature $T_i$, with a process that restores the initial state (nothing must be changed in the universe). Is it possible? Strictly speaking, no, but we can imagine a procedure that, as limiting result, reach the goal. Of course, we can put $\xi$ in thermal contact with an identical body with temperature $2T_f-T_i$ and then with one with temperature $2T_i-T_f$ (if $T_i>T_f/2$). In this way we reach the goal to bring the $\xi$ temperature from $T_i$ to $T_f$ and then again to $T_i$, but at the price of having changed the universe: the two auxiliary bodies experience a change in temperature $2T_f-T_i\to T_f$ and $2T_i-T_f \to T_i$.
One may think to bypass this issue by employing two thermal reservoirs instead of bodies with finite heat capacity. Their immense heat capacity would allow the body to be heated and then cooled, leaving the universe in its initial state. But this approach is flawed: during the process a finite quantity of energy has transferred from one thermal reservoir to another, and even if we can minimize the temperature variations between the initial and final state (by choosing sufficiently large thermal capacities for the reservoirs), a finite amount of energy has unquestionably changed its position: the universe is not returned to its initial state. The fact that we can approximately restore the same energy density as the beginning, is irrelevant. This being the case, reversibility is not guaranteed. It is not necessary to investigate this aspect here, but a deeper analysis shows that the process just described with thermal resevoirs is not reversible: there was a finite increase in entropy of universe (but discussing entropy without first having demonstrated that the heat exchange between bodies at very similar temperatures is reversible, it would be circular).
Nevertheless, there is a method to achieve the goal of performing a heating and cooling cycle for $\xi$, leaving at the end the universe in its initial state: it is sufficient to use a sort of long "thermal chain" of auxiliary bodies with temperature into the range $T_i \leftrightarrow T_f$. By using a such long "chain", the body $\xi$ can be brought from $T_i$ to $T_f$ and back to $T_i$, without producing any net change in the universe. Looking at figure below the reader can guess the methods of the thought experiment, which I will explore in detail in the next sections. To simplify the calculations, I will assume that the auxiliary bodies of the thermal chain have the same heat capacity as the body $\xi$.
The heating process
Proof that the equilibrium temperature when $\xi$ is put in thermal contact with $n^\textrm{th} $ auxiliary body is (2)
Let's suppose to have $N$ bodies identical to $\xi$ (or anyway with the same heat capacity) with temperatures
\begin{equation}
T_i + \frac{T_f-T_i}N \qquad
T_i + 2\frac{T_f-T_i}N \qquad \dots \qquad
T_i + (N-1)\frac{T_f-T_i}N \qquad
T_f \quad \quad \tag{1}
\end{equation}
and imagine to put subsequently $\xi$ (initially at temperature $T_i$) in thermal contact to these bodies (first to the body at temperature $T_i + (T_f-T_i)/N$, then to the body at temperature $T_i + 2(T_f-T_i)/N$, etc.). The process is schematically represented in figure (a tilde show that temperature of intermediate body is a little perturbed).
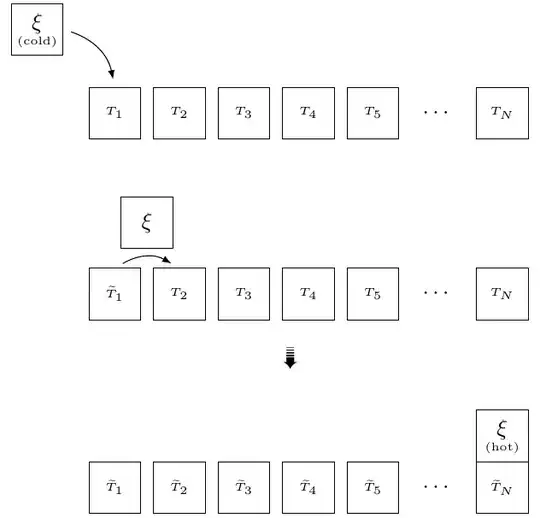
I claim that the equilibrium temperature when $\xi$ is put in thermal contact with $n^\textrm{th} $ auxiliary body is given by
\begin{equation}
\frac{\left( 2^n(N-n+1) -1 \right) T_i +\left( {2^{n}} \left( n-1\right) +1\right) T_f }{ {2^{n}} N } \tag{2}
\end{equation}
where $N$ is the total number of the bodies in the thermal chain, while $n$ is the particular body of the step we are considering, that has temperature
\begin{equation}
T_i + \frac{n}{N} (T_f-T_i) \tag{3}
\end{equation}
I'll proof this claim exploiting mathematical induction.
- The formula (2) works if $n=1$ because it is easy to see that after thermal contact with the first body, the equilibrium temperature is
\begin{equation}
\frac{\left( 2 N-1\right) T_i + T_f }{2 N} \tag{4}
\end{equation}
- If the equilibrium temperature when $\xi$ is put in thermal contact with $n^\textrm{th} $ auxiliary body is given by (2), then its equilibrium temperature when it is put in thermal contact with $(n+1)^\textrm{th} $ auxiliary body, that has temperature $T_i + (n+1)(T_f-T_i)/N$, is given by the average value:
\begin{equation}
\frac{\left( 2^{n+1}(N-n) -1 \right) T_i +\left( {2^{n+1}}n+1\right) T_f }{{2^{n+1}} N } \tag{5}
\end{equation}
but this is exactly what we find if we change $n$ to $n+1$ in (2). This ends the proof.
Please note that calculating $N\to\infty$ in (2) is useless because if $n$ is finite and we use infinite auxiliary bodies, we cannot move from thermal neighborhood of the initial state of $\xi$, and the limit gives $T_i$.
Before making $N$ diverging we must to calculate the final temperature putting $n=N$:
\begin{equation}
\frac{\left( {2^N}-1\right) T_i +\left({2^N} \left( N-1\right) +1\right) T_f }{{2^N}N } \tag{6}
\end{equation}
This gives $T_f$ if $N\to \infty$ so we reached the goal of bringing $\xi$ to temperature $T_f$ (strictly speaking the temperature $T_f$ is never reached with this process, but the point is that we can get close $T_f$ as we want, if we increase the number of auxiliary bodies: this is what we proved now taking the limit).
Proof that every thermal jump, in heating process, is infinitesimal
We can wonder if in the limit $N \to \infty$ (large number of auxiliary bodies) every thermal jump of $\xi$ is always infinitesimal. It is intuitive but to prove this formally let's consider the parameter $x=n/N$ (we have $0<x\leqslant 1$: $x$ is the thermal position, so to speak, of $n^\textrm{th}$ auxiliary body of the thermal chain). This will allow to calculate the final temperature of every auxiliary body in the chain, when $N$ diverges. Substituting $n$ with $xN$ in the equilibrium temperature of $n^\textrm{th}$ auxiliary body, given by (2), we find
\begin{equation}
\frac{ \left( 2^{Nx} (1+N(1-x)) -1\right) T_i + \left( 2^{N x} \left( N x-1\right) +1\right) T_f}{2^{N x} N } \tag{7}
\end{equation}
With the limit $N \to \infty$ we get $T_i+x(T_f-T_i)$, i.e. $T_i+n(T_f-T_i)/N$, but this is the initial temperature of the $n^\textrm{th}$ auxiliary body, as you can see looking (1). This is important: we found that in that limit all thermal jumps done by $\xi$ in the thermal chain are infinitesimal (they can be done as small as we want taking more and more auxiliary bodies).
The cooling process
Proof that the equilibrium temperature when $\xi$ is put in thermal contact with $(N-i)^\textrm{th} $ auxiliary body is (8)
Let's take a look to what happens doing the reverse process, that is putting in thermal contact $\xi$ with the auxiliary bodies (that in the first part of the thought experiment have changed their temperature), traveling the chain to lower and lower ones. This time I don't report figures but reader certainly understands how the thought experiment works. I claim that after thermal contact with $(N-i)^\textrm{th} $ auxiliary body the equilibrium temperature is given by
\begin{equation}
\frac{ \left( {2^N} \left( {2^{i}} i +1\right) -\frac{{2^{2 i+1}}+1}{3}\right) T_i+\left( \frac{{2^{2 i+1}}+1}{3}+{2^N} \left( 2^i(N-i)-1\right) \right) T_f }{ 2^{N+i} N } \tag{8}
\end{equation}
Again, I'll proof this claim exploiting mathematical induction.
- Substituting $n$ with $N-1$ in the formula (2) we find that after heating process the $(N-1)^\textrm{th} $ auxiliary body has temperature
\begin{equation}
\frac{\left( {2^{N+1}}-2\right) T_i+\left( {2^N} \left( N-2\right) +2\right) T_f}{{2^N}N } \tag{9}
\end{equation}
and putting in thermal contact with $\xi$ (that at the end of the first part of the thought experiment has temperature given by (6), as we found) we find an equilibrium temperature that can be rearranged in
\begin{equation}
\frac{ 3 \left( {2^N} -1 \right) T_i+\left( {2^N} \left( 2 N-3\right) +3\right) T_f }{{2^{N+1}} N} \tag{10}
\end{equation}
This is the same temperature that we find by substituting $i$ with $1$ in (8), so the formula (8) works for the first thermal contact in the cooling process.
- After the heating process, the $(N-i-1)^\textrm{th} $ auxiliary body assume the temperature given by (2) with $n=N-i-1$:
\begin{equation}
\frac{ \left( {{2}^{N-i-1}} \left( i+2\right) -1\right)T_i +\left( {{2}^{N-i-1}} \left( N-i-2\right) +1\right) T_f }{ 2^{N-i-1} N } \tag{11}
\end{equation}
If the equilibrium temperature when $\xi$ is put in thermal contact with the auxiliary $(N-i)^\textrm{th} $ auxiliary body is given by (8), then its equilibrium temperature when it is put in thermal contact with $(N-i-1)^\textrm{th} $ auxiliary body, that has temperature (11) reached in the heating process, is given by the average one
\begin{equation}
\frac{\left( {{2}^{N}} \left( {{2}^{i+1}} \left( i+1\right) +1\right) -\frac{{{2}^{2 i + 3}}+1}{3} \right) T_i + \left( \frac{{{2}^{2 i + 3}}+1}{3}+{{2}^{N}} \left({{2}^{i+1}} (N-i-1) -1\right) \right) T_f}
{2^{N+i+1} N } \tag{12}
\end{equation}
but this is exactly what we find if we change $N-i$ to $N-i-1$ (i.e. $i$ to $i+1$) in (8). This ends the proof.
Now we are ready for the final step. The core of the whole answer is synthesized in the title of the next section.
Proof that the final state of the system is equal to the initial one, and that every thermal jump, in cooling process too, is infinitesimal
Making $N \to \infty$ in (8) we get $T_f$, but this is a situation analog to the one we encountered before: this limit is not interesting because $i$ and $N$ must be sent to infinity, so to speak, together (or we will inevitably end up squeezed at the hot edge of the thermal chain). We can do it by exploiting the variable $x=(N-i)/N$ (it has always the same meaning as before: $x$ is the "position", in the thermal chain, of the body considered, expressed as number between $0$ and $1$, the cold and the hot limit respectively). By substituting $i$ with $N(1-x)$ in (8) we can write in this way the final temperature of the body characterized by $x$
\begin{equation}
\frac{
\left(
2^{N(1-x)}N(1-x)+1-\frac{2^{N(1-2x)+1}+2^{-N}}{3}
\right) T_i +
\left(
\frac{2^{N(1-2x)+1}+2^{-N}}{3} + 2^{N(1-x)} Nx - 1
\right) T_f}{2^{N(1-x)} N} \tag{13}
\end{equation}
Considering that $0< x \leqslant 1 $, when $N\to\infty$ this quantity approaches to
\begin{equation}
T_i+x(T_f-T_i) \tag{14}
\end{equation}
So, we again have that when the process is done coming back, bringing the temperature of $\xi$ from $T_f$ to $T_i$, the equilibrium temperature of every body of the thermal chain is the same as the initial temperature.
Clearly all this claims have a meaning if we consider the limiting case of many auxiliary bodies, and strictly speaking the starting temperature are never reached again in this thought experiment.
Why all the energy is returned to its original position
As mentioned in the section 2, in order to talk about a reversible process we must be sure that everything can be restored to the original situation, and in particular that all the energy transferred in the process from one body to another can return to the initial bodies. As regard to the auxiliary bodies the problem does not exist because they only undergo two infinitesimal heat flows, therefore the energy variation can be made as small as desired by increasing the length of the thermal chain. The situation is more delicate regarding the body $\xi$, which undergoes infinite infinitesimal heat flows. In reality, if we assume that the coefficient of thermal expansion is small, the fact that $\xi$ undergoes two opposite temperature variations, exhausts the problem: any work done by the bodies on the surrounding system is supposed negligible and the energy content of the bodies can only vary as a result of heat flows, directly proportional to temperature variations. Nevertheless if the reader wants to explicitly check the calculations (after all by dealing with limiting cases one could be misled, as the case of heat reservoir shows) I'll report them here.
Let's consider the heating and the cooling of $\xi$ separately.
During the heating, the heat flowed to $\xi$ when it moves from $n^{\textrm{th}}$ to $(n+1)^{\textrm{th}}$ body, is found by taking (5) minus (2), and then multiplying by heat capacity $C$:
\begin{equation}
Q_n = C \left( 1 - \frac{1}{2^{n+1}} \right) \left( \frac{T_f - T_i}{N} \right) \tag{15}
\end{equation}
By summing on $n$ from $1$ to $N$ we find the total heat flowed to $\xi$:
\begin{equation}
Q_\textrm{heating} = C \left( N + \frac{1}{2^{N+1}} - \frac{1}{2} \right) \left( \frac{T_f - T_i}{N} \right) \tag{16}
\end{equation}
Taking $N\to\infty$ we find the unsurprising result $C(T_f-T_i)$.
During the cooling, the (negative) heat flowed to $\xi$ when it moves from $(N-i)^{\textrm{th}}$ to $(N-i-1)^{\textrm{th}}$ body, is found by taking (12) minus (8), and then multiplying by heat capacity $C$:
\begin{equation}
Q_i = C\left(1 - \frac{1}{2^{i+1}} + \frac{1-2^{2i+2}}{3\cdot 2^{i+N+1}} \right) \left( \frac{T_i - T_f}{N} \right) \tag{17}
\end{equation}
By summing on $i$ from $0$ to $N-1$ we find the total heat flowed to $\xi$:
\begin{equation}
Q_\textrm{cooling} = C \left(
2^{1-N} + N - \frac{5}{3} - \frac{1}{3\cdot 2^{2N}}
\right) \left( \frac{T_i - T_f}{N} \right) \tag{18}
\end{equation}
Taking $N\to\infty$ we find a result opposite: $C(T_i-T_f)$.
We conclude that $\xi$ gives off the same heat that it receives: in the limit $N \to \infty$ all the energy has returned to where it originally was.
Conclusions
The essence of what was treated here is that starting from the trivial hypothesis that 2 identical bodies at temperature $T_1$ and $T_2$ reach the equilibrium at temperature $(T_1 + T_2)/2$, we can show with a thought experiment that we can make finite temperature change of a body $\xi$ exploiting a thermal chain of many (ideally infinite) bodies, and we have that
- all thermal jumps of the body $\xi$ are infinitesimal;
- The body $\xi$ can be brought from temperature $T_i$ to temperature $T_f$ (with $T_f-T_i$ finite, if auxiliary bodies are infinite) and then brought again to $T_i$, without any change in the universe.
That's why infinitesimal heat flux are reversible.
Where the formulae proved by mathematical induction come from
As often happens with proofs that exploit mathematical induction, reader can wonder where the formulae proved were found, they looks "fallen from the sky". It is not necessary to answer to this question to make the proof "more rigorous", and a completely legitimate answer could be "it was found by a stroke of luck". However clearly this is not the answer here, and it could be interesting to show the reasoning that lead me to consider the validity of (2) and (8).
How formula (2) was found
Putting $\xi$ in thermal contact with the first body, I find the equilibrium temperature
\begin{equation}
\frac{\left( 2 N-1\right) T_i + T_f }{2 N} \qquad (n=1) \tag{(4)}
\end{equation}
Putting then in thermal contact with the second body, and going on with next bodies, I got these equilibrium temperatures
\begin{equation}
\frac{\left( 4 N-5\right) T_i +5 T_f }{4 N} \qquad (n=2) \tag{19}
\end{equation}
\begin{equation}
\frac{\left( 8 N-17\right) T_i +17 T_f }{8 N} \qquad (n=3) \tag{20}
\end{equation}
\begin{equation}
\frac{\left( 16 N-49\right) T_i +49 T_f }{16 N} \qquad (n=4) \tag{21}
\end{equation}
\begin{equation}
\frac{\left( 32 N-129\right) T_i +129 T_f }{32 N} \qquad (n=5) \tag{22}
\end{equation}
\begin{equation}
\frac{\left( 64 N-321\right) T_i +321 T_f }{64 N} \qquad (n=6) \tag{23}
\end{equation}
It is clear what is happening with denominators, but with Google we can also conjecture the trend of numerators.
Exploiting "The online encyclopedia of integer sequences" we guess that the sequence $1,5,17,49,129,321,\dots$ is given by $\{ (n-1)\cdot 2^n + 1 \}$. This inspire the formula (2) for the equilibrium temperature when $\xi$ is put in thermal contact with the $n^\textrm{th}$ auxiliary body.
The conjecture is then rigorously proven in the answer.
How formula (8) was found
We found that if after the whole heating process, $\xi$ is put in thermal contact with the $(N-1)^\textrm{th}$ auxiliary body, the equilibrium temperature is given by (10). I'll transcribe here without collecting $3$ for reasons that will appear clear
\begin{equation}
\frac{ \left( 2^N \cdot 3 -3 \right) T_i+\left( {2^N} \left( 2 N-3\right) +3\right) T_f }{{2^{N+1}} N} \qquad (i=1) \tag{10}
\end{equation}
Putting then in thermal contact with $(N-2)^\textrm{th}$ auxiliary body, that after the first part of the thought experiment assume temperature given by (2) with $n=N-2$,
\begin{equation}
\frac{ ( 3 \cdot 2^{N-2} - 1) T_i +\left( 2^{N-2} \left( N-3\right) +1\right) T_f}{2^{N-2} N} \tag{24}
\end{equation}
we find an equilibrium temperature
\begin{equation}
\frac{ \left( 2^N \cdot 9 -11\right) T_i+\left( 2^N \left( 4 N-9\right) +11\right) T_f }{{2^{N+2}} N} \qquad (i=2) \tag{25}
\end{equation}
Going on in this way, after thermal contact with $(N-3)^\textrm{th}$ and $(N-4)^\textrm{th}$ auxiliary bodies, we find
\begin{equation}
\frac{\left( 2^N \cdot 25 -43\right) T_i+\left( 2^N \left( 8 N-25\right) +43\right) T_f }{{2^{N+3}} N} \qquad (i=3) \tag{26}
\end{equation}
and
\begin{equation}
\frac{ \left( 2^N \cdot 65 -171\right) T_i+\left( 2^N \left( 16 N-65\right) +171\right) T_f }{{2^{N+4}} N} \qquad (i=4) \tag{27}
\end{equation}
Exploiting "The online encyclopedia of integer sequences" we guess that, reasonably, $3,9,25,65$ is the sequence $\{n\cdot 2^n +1\}$ while $3,11,43,171$ is the sequence $\left\{(2^{2n+1}+1)/3\right\}$. So we are led to think that after thermal contact with $(N-i)^\textrm{th} $ auxiliary body the equilibrium temperature is given by (8). Again, the conjecture is rigorously proven in the answer.
$\quad$
[MAXWELL] J. C. Maxwell. *Theory of heat Dover, 2001 (republication of 9$^\textrm{th}$ edition of 1888, this edition included Maxwell's additions and corrections to his original text of 1871).
[PLANCK] M. Planck. *Traise on Thermodynamics, Dover, 1969 (republication of the 3$^\textrm{rd}$ revised edition originally published in 1917).
[FERMI] E. Fermi. *Thermodynamics. Dover, 1956 (republication of the work originally published in 1937).
[FEYNMAN] R. Feynman. *The Feynman Lectures on Physics. Addison-Wesly, 2005 (revised and extended 1964 edition).
[MORAN-SHAPIRO] M. J. Moran; H. N. Shapiro. *Fundamentals of Engineering Thermodynamics. John Wiley & Sons, 6$^\textrm{th}$ edition, 2010.
[STEANE] A. M. Steane. *Thermodynamics. Oxford University Press, 2017.
