The third law of thermodynamics is that the entropy of a system approach a constant value when the temperature goes to zero, this value is independent from any parameter that characterize the system.
A consequence that can be derived from this law is that, quoting H. B. Callen is that:
... no reversible adiabatic process starting at nonzero temperature can possibly bring a system to zero temperature.
To understand why this is a consequence of the third law of thermodynamics, consider the entropy as a function of the temperature, $T$, and of some other parameter, $X$ (for simplicity consider a closed system). So, we have $S=S(T,X)$.
Given a value of the parameter $X$, the entropy is an increasing function of the internal energy, and, so, of the temperature. The $S-T$ diagram for two different values of the parameter $X_1$ and $X_2$, will be something like the one below:
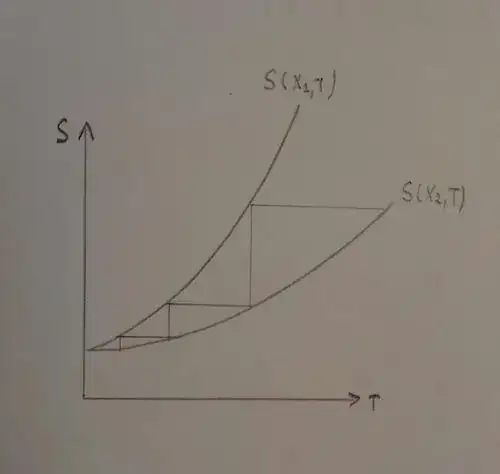
as you can see:
an adiabatic reversible process is also isentropic, because $dS=\delta Q_{rev}/T=0$, and so, it is represented by an horizontal line. If we change the value of the parameter, in a reversible manner, from $X_2$ to $X_1$, the temperature decrease.
an isothermal transformation is represented by a vertical line. If we switch back the parameter, from $X_1$ to $X_2$, keeping the temperature constant, the entropy increase.
So, if the horizontal and the vertical transformations are repeated many times, the temperature decreases, but, as you can see, the more $T$ gets close to $0k$, the less it decreases. It would require infinite transformations to go to absolute zero.
Then, can we achieve $T=0k$ if we change the parameter, in an irreversible manner? No. If the parameter changes, from $X_2$ to $X_1$, and the system is adiabatic, $dS \ge Q/T_{surr}=0$. So, in the irreversible transformation, the system state moves from an initial one ($A$) to a final one ($B'$) whose entropy and temperature are larger than those reached through a reversible transformation ($B$). Loosely speaking, an in irreversible transformation adding friction and dissipation is even worst.
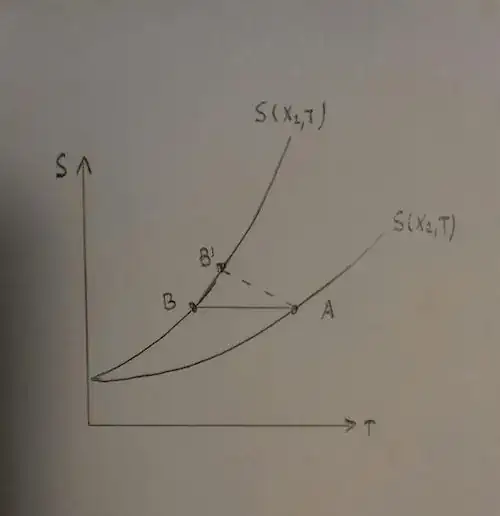
Until now we have considered an adiabatic system, what if the system is not adiabatic? Since we don't have any reservoir at absolute zero, during the cooling process toward zero, at a certain point the environment will become hotter than the system. So heat will enter into the system making things worse.
Is it impossible to reach absolute zero? It may be impossible, but actually, if that is the case, it's not a consequence of the third law of thermodynamics. Indeed the third law involve that it is impossible to reach absolute zero by changing the system parameters, however, there could be other ways to create a very cold system. For example, we could create directly a very cold system, instead of creating one and cool it down (i.e. the laser cooling, in which a flux of gas is slowed down, by a laser, into a very cold gas).
Finally, there may be issues in the concept of reaching absolute zero. For example, it would require an infinite precision. I think this quote from H.B. Callen in on the point:
The question of whether the state of precisely zero temperature can be realized by any process yet undiscovered may well be an unphysical question, raising profound problems of absolute thermal isolation and of infinitely precise temperature measurability.
So, one problem in reaching $0k$ is that it would require an infinite precision. However, when it comes to continuous physical quantities, a measurement is intended with a certain uncertainty.

