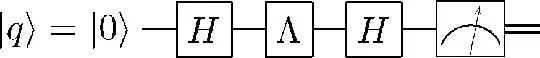A continuation of Understanding the quantum eraser from a quantum information stand point
What quantum circuit would correspond to delayed choice? In particular, the decision of whether to not to destroy the which-way information is made after we check whether it has interfered or not.
Here is an example of a delay choice experiment:
Erasure occurs at $BS_c$.
NOTE: This answer has now been merged into Understanding the quantum eraser from a quantum information stand point (part IV).
Let me start by copying the first part of my previous answer which describes the circuit model of a double-slit or other interference experiment; then, I will try to describe the delayed choice setting (the way I understand it).
An interferometer corresponds to the following circuit:
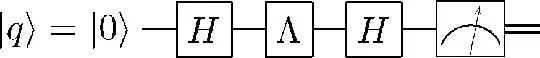
Here, the first $H$ puts the qubit in the superposition of both paths/slits -- the states $\vert0\rangle$ and $\vert1\rangle$ correspond to the two paths/slits --, the matrix $$ \Lambda = e^{i\phi/2}\vert0\rangle\langle0\vert + e^{-i\phi/2} \vert1\rangle\langle1\vert $$ introduces a phase shift between the two paths (this can e.g. be a function of the position on the screen, or the relative length of the interferometer arms), and the second $H$ makes the two paths interfere. If the output qubit is measured in state $\vert0\rangle$, the interference is constructive, otherwise desctructive.
You can easily check that this yields an interference pattern which varies like $\mathrm{prob}(0)=\cos(\phi)^2$.
In the delayed choice experiment, we want to copy the which-way information onto an auxiliary qubit (just as explained in the previous answer, part II), then measure the "interference pattern", and only then decide if we erase the information.
This is described by the following circuit:
Here, we copy the which-way information onto the qubit $c$ before traversing the interferometer. After the interferometer, the $H$ makes the two paths interfere, and we measure. Note that at this point this is nothing but the part II of the previous answer and thus, $\mathrm{prob}(0)=1/2$. (In particular, there is no interference whatsoever observed.)
Now we measure the which-way qubit. There are two ways of measuring it:
Measurement in the $\vert0\rangle$, $\vert1\rangle$ basis reveals the which-way information. Going through the math, you can easily see that in this case, the distribution for $q$ is $\mathrm{prob}(0)=1/2$ for both outcomes $c=0$ and $c=1$.
(Note that the state before the measurement on $q$ does depend on the outcome of $c$ -- you can understand this by either changing the order of the two measurements, or by saying that the state before the measurement is entangled.)
Let us now instead measure $c$ in the $\vert+\rangle$, $\vert-\rangle$ basis. If we obtain outcome $\vert+\rangle$, we have effectively erased the which-way information. This can be understood by moving the measurement all the way to the CNOT, and noting that a CNOT in this setup, followed by a projection onto the $\vert+\rangle$ state on the target qubit, corresponds to the identity on the control qubit.
If we obtain $\vert+\rangle$, the (conditional!) probability distribution on $q$ will be thus $\mathrm{prob}(0)=\cos(\phi)^2$.
What happens if we obtain $\vert-\rangle$? In this case, one can easily check that the CNOT + projection yields a Pauli $Z$, i.e., there is an additional phase shift of $\pi$ introduced between the two paths of the interferometer. This is, in this case, we will still have interference, but the interference pattern will be shifted by half a spacing, i.e., $\mathrm{prob}(0)=\sin(\phi)^2=1-\cos(\phi)^2$.
So what does this teach us? As long as we don't know the measurement outcome on the $c$ qubit, we will see the average of both interference pattern, which is nothing but $$ \tfrac{1}{2}\Big[\sin(\phi)^2+\cos(\phi)^2\Big]=\frac{1}{2}\ , $$ and thus just the same as if we would not have measured $c$, or measured in the which-way basis. This, of course, makes a lot of sense -- observations on $q$ should not depend on whether (and how) $c$ has been measured.
Thus, in order to reveal the interference pattern when erasing the which-way information, we have to carry out the experiment repeatedly (a single run will clearly not allow to determine $\mathrm{prob}(0)$ or to see interference fringes). Once we have done so, we need to take all outcomes (clicks) on $q$ where the erasure works (i.e., where we obtained $\vert+\rangle$ on $c$) and look only at those, i.e., the conditional probability distribution $\mathrm{prob}(q=0|c=+)$. Once we do so, but only then, we will see an interference pattern. Nothing magic going on here.
I will refrain from interpretations here, but depending on one's personal interpretation, this might have some implications what the photon "does" when passing the double slit.
