Can Kirchoff's loop rule be applied in a scenario involving an inductor? Kirchoff's loop rule states that the closed loop integral $\oint\mathbf{E}\cdot d\mathbf{l}$ is equal to zero. But, in a situation with an inductor, a changing magnetic flux is involved which means that the electric field is nonconservative and the closed loop integral $\oint\mathbf{E}\cdot d\mathbf{l}$ is not zero. I watched MIT professor Walter Lewin's lectures on inductance and Faraday's law and he emphatically states that Kirchoff's loop rule cannot be used in this situation. Yet, most textbooks (University Physics, Giancoli, Berkeley Physics, etc.) use the loop rule anyways (setting the "voltage drop" across the inductor to be $-L\frac{di}{dt}$ and setting the sum of all the voltage drops to be zero). Now I am very confused. Any help would be greatly appreciated!
4 Answers
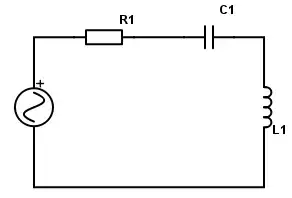
OK, in this video you've kindly provided me, Lewin essentially talks about this circuit:
The easy rule of thumb that's common to all electrical engineers is to say: a current $I$ goes through this loop, causing a voltage drop $R I$ across the resistor, a voltage drop $\int_0^t dt~I(t)/C$ across the capacitor (assuming it is uncharged at $t=0$), and a negative voltage drop $-L \frac{dI}{dt}$ across the inductor, which then by Kirchoff's rules must sum to 0.
Why is Lewin upset with these matters?
Lewin is saying that this last point of interpretation is essentially cheating, which we're totally allowed to do in physics; but he points out why it would be hella-confusing to a student with a very simple thought-experiment: imagine that the coil of wire which constitutes the inductor has zero resistance. Since it has zero resistance, an electric field therein cannot exist; it would move an infinite amount of current whereas we know that the current is finite: therefore the electric field inside the inductor's wire must be 0. So how can we speak of a voltage difference if the electric field is zero?! This is the challenge that Lewin doesn't want to push past. He wants his students to think "the electric field is the gradient of the electric potential, the electric field is for sure zero here, the potential therefore doesn't meet up as you go around this loop, but that's okay because Kirchoff's rule is wrong. And he gets quite passionate that this is the best way to view this, and then insists on using the "wrongness", which has a magnitude of $L~dI/dt,$ to analyze the system in place of a voltage.
But electrical engineers might fire back that we can just speak of an "effective voltage" across $L$ defined by connecting a potentiometer across the inductor -- you'll measure the given voltage! Easy-peasy. (We can't always use this method -- always when you're measuring, a potentiometer can interfere with the system that it's measuring, and we just assume in practice that this interference is small and that an "ideal" potentiometer solves this problem. But here it simplifies things.) And he'll say "yeah, but then you shoot your students in the foot because they run into this inductor which is a perfect conductor and they expect a changing electric field going through it, and then they complain to you about infinite currents! So they just have the idea that they don't understand how anything works! That's criminal. That's putting magic into your electrical engineering classroom."
How can a better understanding of physics solve this?
Well, let's put on our mathematician pants. It turns out that in general, $\vec E$ is not $-\nabla \phi$. So $\phi$ can vary across the wire while $\vec E$ is zero. This happens routinely when there are changing magnetic fields nearby.
The four Maxwell equations are (in SI units since I don't want to jar anyone too much):$$\begin{array}{ll} \nabla \cdot E = \rho/\epsilon_0 & \nabla \times E = - \dot B\\\nabla\cdot B = 0&\nabla\times B=\mu_0 J + \mu_0 \epsilon_0 \dot E\end{array}$$where $\dot X = \partial X/\partial t$. The bottom-left equation says that there are no magnetic charges (monopoles) like there are for the electric field above it (which is the generalization of Coulomb's law). In fact, it turns out to always guarantee that $B = \nabla\times A$ for some vector field $A$ commonly called the vector potential. So $B$ curls around some field lines of vector potential, which go "around the loop" with the wire in $L,$ forcing the $B$ to take a path through the loops.
Then the top-right Maxwell equation -- which is Faraday's law! -- actually says that $\nabla \times (E + \dot A) = 0$ so that we can for sure say that $E = -\dot A - \nabla \phi$ for some scalar potential $\phi$. These two quantities are not unique; there are "constants of integration": basically, if we add some $\nabla \psi$ to $A$ we for sure will preserve $B$, and we will also preserve $E$ if we simultaneously add $\dot\psi$ to $\phi$. This is called the "gauge freedom" for the system. Let's ignore that and just pretend that we've already solved this problem and chosen the "most obvious" $A$ and $\phi$, which probably means that $\dot A = 0$ or some such for these other wires and the $R$ and $C$ and $V(t)$ parts of the above circuit.
Well, now it makes total and complete sense to call $\phi$ the "voltage" and it corresponds to what you'll measure across the terminals of $L$ with a potentiometer (if you carefully make sure that $\dot A = 0$ along the potentiometer's loop). However, if $\dot A \ne 0$ then you can often have $E \ne -\nabla\phi.$ In fact, our equations say that $\dot A$ works basically like a second $E$ field as a source of voltage differences. In summary:
- Kirchoff's laws work if you use "effective voltage," which is defined as a line integral of $E + \dot A$, where $A$ is the magnetic vector potential.
- There turn out to be a lot of definitions of $A$ and therefore of $\phi$ but this probably doesn't matter much.
- Inductors are cases where $\dot A = L \dot I,$ providing an effective voltage without an electric field.
- You can still think of "electric potential" as "something which tends to causes electrons to flow," but with the caveat that they might not if the vector potential is changing appropriately so as to fight it.
Let us consider the following circuit.

Kirchhoff's loop rule, as you said, states
$$\oint\mathbf{E}.d\mathbf{l} = 0$$
when the magnetic field is constant(with time). When we talk about circuits with inductors and hence changing magnetic field, it is indeed wrong to use Kirchhoff's loop rule from a conceptual point of view.
Then what should we do? Just take the changing magnetic field into account in the above equation. Kirchhoff's loop rule is a special case of one of Maxwell's equations which is,
$$\oint\mathbf{E}.d\mathbf{l} = -\frac{d\phi_B}{dt}.$$
This equation is true irrespective of whether we are dealing with magnetostatics. Now integrating such that $d\mathbf{l}$ is directed from positive to the negative terminal of the source (at some instant of time) inside the source, the left-hand side of the equation is equal to $\varepsilon$ as the electric field is zero everywhere except the source (assuming we integrate along the circuit wires). This is because there is no electric field along the circuit wires as the wires have zero resistance. Now for calculating the right-hand side of the equation, note that $\phi_B = -iL$ with $i$ being the current in the circuit. The minus sign comes because the direction of the current is opposite to that of the direction of $d\mathbf{l}$ in our integration*. Thus we get the following equation:
$$ \varepsilon = i\frac{dL}{dt} $$
This is the same thing we would get if we used Kirchhoff's loop rule as it is done in many books which you pointed out in your question.
*The minus sign and the directionality might initially seem a little confusing. Still, thinking about it with $\phi_B = \mathbf{B.A}$ in mind (where $\mathbf{B}$ is the magnetic field whose direction is given by the direction of the current and $\mathbf{A}$ is the area of the circuit whose direction is given by the direction of $d\mathbf{l}$) should make it easier to understand.
PS: This is my first answer on stack exchange. Please let me know if I am wrong on any point.
- 31
Physicists have a slightly different (and in my opinion incorrect) way of deriving nodal circuit diagrams than engineers, which would make his statement correct because the circuit diagram would imply that the wires form loops of a finite area, but this way of thinking breaks the usefulness of circuit diagrams in fundamentally undesirable ways.
If you think of the "wire" in a nodal circuit as a ideal physical wire instead of a topological connection diagram, then you are running into the problem that Lewin mentions. Now you are't denoting just the topology of the circuit, but also a "flattened" version of its geometry. This, of course, is insufficient to solve any realistic electromagnetic problem. The real components denoted by a circuit diagram are not arranged the same way on a circuit board or in their often three dimensional assembly as they are being shown in the circuit diagram. The diagram should always arrange them in a logical way that makes the function and operational principle of the circuit easily understandable. The actual implementation can be as convoluted as required by the mechanical constraints of the hardware, but that shouldn't show in the diagram.
If you wanted to include the quasi-static electromagnetic effects that follow from next higher approximation of wires as real, albeit small inductors, capacitors and resistors, then you would have to add a load of new information to the circuit diagram, denoting each connection's resistance, loop self-inductances, mutual inductance of all loops to all other loops (n*(n-1)/2 values) and all the capacitance coefficients. This can, of course, be done. High performance circuit simulators can extract these models from printed circuit boards and chip layouts and they can simulate them properly... but not one in a hundred electrical engineers will ever work with these tools and even fewer physicists will (I have, they are horrible, horrible, horrible toolsets and you only use them if you absolutely have to).
Nobody who uses circuit diagrams in practice thinks of a circuit diagram as a geometric description, though. The dimensionality would be wrong, already (2d instead of 3d). Lewin is unlikely to ever do hands on electronics, so he may have the complex scenario described above in mind, but that's not how one would read a circuit diagram. A simple circuit diagram merely shows the topology of the circuit and it doesn't matter how long a particular wire is or how large the loops are. If we need to incorporate that information, we do it by adding discrete components for stray inductances, wire capacitances etc. to those select parts of the circuit where they can not be neglected. We annotate those components with the necessary information about the size of the physical connectivity loops etc.. The same is true for wire resistances. When they matter, we add them as a resistor labeled $R_{wire}$, inductors labeled $L_{self}$, capacitors labeled $C_{stray}$ or so.
To sum it up, Lewin means well by pointing out a real problem, but he gives the incorrect "engineering advice", so to speak. Never think of a circuit diagram as anything but a topological diagram. If you need to go further in the analysis of a real physical piece of electronics, incorporate the higher order analysis as stray elements and preserve the simplicity of Kirchhoff's rules.
- 16,486
Kirchoff's loop rule states that the closed loop integral $\oint\mathbf{E}\cdot d\mathbf{l}$ is equal to zero.
This is a common misconception, found also in well-known textbooks. In fact, there are two variants of this law; and both are different from the above.
Kirchhoff's second circuital law in its original form (as he formulated it) states: sum of all emfs acting on current in a closed path equals sum of terms $R_kI_k$ over all members with resistance $R_k$ and current $I_k$ in the closed path.
This original law is applicable even to circuits with changing magnetic flux. Thus including the circuits with inductors, but also those acted upon by external induced electric field, e.g. circuits near moving magnets, or near some other circuit that produces strong induced electric field (e.g., transfomer). Thus it is a very general physical law (the main idea is the same as the idea of generalized Ohm's law).
The Kirchhoff Voltage Law (KVL) is a modern rule used in electrical engineering to write down circuital equations. It states something very different: that sum of potential drops on all elements in the path equals zero. This is correct generally, but it is applicable only to a narrower set of cases, when we can express the potential drops in terms of current; and that requires that external induced electric field acting on the circuit element has to be negligible, or at least its integral has to be known, which often is not. Thus KVL, while a useful rule, has limited applicability. When in doubt, or dealing with circuits affected by external field, use the original law.
Neither of these two formulations states that for a closed path following the circuit elements, $\oint \mathbf E \cdot d\mathbf l= 0$. Instead, this is a special condition that is valid when rate of change of magnetic flux through the closed path is zero (due to Faraday's law). But both above rules are valid even if this special condition is not satisfied.
Walter Lewin is right that Kirchhoff's law is often taught badly, but he himself commits the sin, because he too works with the misguided assumption that Kirchhoff's law states that $\oint \mathbf E\cdot d\mathbf l = 0$. That is maybe a third meaning of "Kirchhoff's law", which lead people to invent all kind of gymnastics to make it work (deformation of the path to go around the inductors). But it is a bad use of the words "Kirchhoff's law" since it is ahistorical, more complicated than the above, and often leads to misunderstanding of the physics of electric circuits.
- 44,745