Assuming an ordinary hinged door (without any springs), would it take more energy to open it when applying force in the middle of the door (point b), rather than at the end of the door (point a), where the door knob is?
"Opening the door" should be interpreted as accelerating the door to a certain rotational speed.
My own answer is no, since the change in force would be proportional to the distance required to open the door and therefore the total energy would remain the same.
You are right.
To open the door during the same time interval (for pushing at $a$ and $b$), you should induce the same angular acceleration. Since rotation in both cases is about the same axis, this means you need the same torque, this gives $$ \frac{F_a}{F_b} = \frac{r_b}{r_a} $$ where $r$ is the distance from the point of contact to the axis.
However the distance that the force should be applied at $a$ and at $b$ are related because they are arcs of the same angle $$ \frac{r_b}{r_a}=\frac{l_b}{l_a} $$ This implies that $F_a l_a = F_b l_b$ and equal work needs to be done.
The physics 101 answer is no: it takes more force, but it is compensated by the smaller displacement so the energy stays the same. If we start with a static door, and we end up with a door rotating at some speed, the energy into the door is the work done by the force and it must be the same independently from the point where the force was applied
But let's dig a bit deeper! When you apply the force, you also have some reaction force on the hinges, which generate some friction, which dissipates energy. So if you stay closer to the hinges, the higher force will in the end require a bit more energy.
We can also consider the device generating the force. If it is your arm, then we have another effect: the energy consumed by muscles only to generate some force is (somehow) proportional to that force. This happens because more muscle fibres have to contract to generate an higher force. Indeed if you try to close ten doors applying the force very close to the hinges, you will be much more tired than closing ten doors from the handle.
This is also the case with an electric motor: higher force (torque) requires higher current which leads to higher ohmic losses, so more energy is dissipated.
It is generally better to keep the forces down when possible.
The answer is NO.
Change of energy is work i.e $W = \Delta E$ and here the work done is $$W = \text{Torque} \cdot \text{angular displacement}$$ which is equal in both the cases. The only change is one needs to apply more force to achieve the same amount of torque at a smaller radius. $$\text{Force at "b"} > \text{Force at "a"}$$ but not the work done or the energy spent.
To get to a final rotational velocity $\Omega$ is takes the same amount of energy regadless of where you push. Why? Well the final kinetic energy is $K=\frac{1}{2} I \Omega^2$ (where $I$ is the mass moment of inertia about the hinge) and this value does not depend on where you push.
This is kind of a boring result.
What does differ is how much you need to push, and how much reaction the hinges provide. If you only push for a small period of time providing with an impulse $J=\int F(t)\,{\rm d}t$ then the hinges would develop a reaction impulse of $R$.
$$\begin{align} J & = \frac{I \Omega}{a} & R = \frac{I \Omega}{a} - m \Omega \frac{\ell}{2} \end{align} $$
where $a$ is the distance of where I push from the hinges and $\ell$ is the width of the door. Given that $I=m \frac{\ell^2}{3}$ it can be seen that when $a=\frac{2}{3} \ell$ there is no reaction on the hinges. That is called the center of percussion (sweet spot).
Now the impulse $J=F \Delta t$ can be viewed as an average force $F$ applied for a small time $\Delta t$. If the time of pushing is fixed, then $$F = m \frac{\Omega \ell^2}{3 a \Delta t} $$ which means the further away from the hinge the less the force (duh!).
Now if the distance $\delta$ by which the force is applied is fixed ($\Delta t = \frac{\delta}{v} = \frac{\delta}{a \Omega}$) the force is $$F = m \frac{\Omega^2 \ell^2}{3 \delta} $$ which does not depend on the distance $a$. This can be explained since force over distance is work, which goes into kinetic energy, since the goal is the same kinetic energy, it takes the same amount of work. If the distance is fixed then the force must be fixed also to get to the same work.
The two equations of motion I used are
Figure 1. Door sketch from the top
...would it take more energy to open it when applying force in the middle of the door rather than at the end of the door
When you push a free body it will translate (yellow arrows) and rotate (white arrows) on the center of mass (C, CM, CoM)
at b (CM) it will only translate. If it is hinged it can't translate and is forced to rotate on one tip: pushing at a (the handle) you are following the natural outcome. As you get nearer to the hinge there will be an increasing opposing force (red arrows) contrasting the applied force (black arrows).
The resulting Net force (green arrows) is the outcome, which is different at every point, the max resistance being, of course, near/at the hinge.
so your answer is "Yes, it would take more energy"? – JonathanReez
Because of the definition of mechanical work the energy that produces same ω must be the same, but that definition accounts only for the net force, the last proposition warns you: "Notice that only the component of torque in the direction of the angular velocity vector contributes to the work." other components in other directions, or other opposing forces (which you call increased friction) are not accounted for.
The accepted answer does not take into account the real opposing forces:
it can be seen that when a = 2/3 ℓ, there is no reaction on the hinges. That is called the center of percussion (sweet spot). .. If the door is free floating in space and you hit it at the CoP it will rotate about the end of the door (where the hinges would have been). – ja72
That is not true, that urban legend spread by wikipedia is quickly disproved (I imagine) applying his own formulas, which produce his trochoid
the only difference is that at CoP the free 'door' describes a common and from there to the tip a prolate trochoid (where the 'kick' on the wrist of a batter is less 'sweet' because there are more vibrations and, above all, is in the opposite direction). But there are always two opposing forces contrasting the motion and not one (R = J - v).
The opposing forces act before you get $J_{door} = L/a$ and can be deduced considering the conservation laws. Lastly, you could open the door near the hinge with same energy if you could use (not a hand or a kick but) a 40-ton tank on a millimeter, but if you managed that unrealistic task, that would bring down the wall, and probably also the house.
Torque=(R) x (F) Energy req. to rotate=(T).(Theta), Ta=Tb, ONLY Fa is less than Fb. & T at Hinge=0, it'll not rotate there. The force required will increase from A to hinge point. Energy needed hence is const from A to hinge(except hinge point). [Ta means torque applied at A]
If you open a door by pushing it near the hinge, you apply greater force than when you push it near the outside edge, which requires lesser force since the width of the door acts as a lever and force multiplier. As the friction of the hinge and the weight of the door are equal in both cases, and assuming displacement is the same, net energy transferred to the door is the same in both cases, but only if the speed of the door swinging open is the same in both cases.
Kinetic energy = 0.5 * mass * v^2
You could also solve this problem by using torque. Although energy is a scalar and torque is a vector, they are both expressed in newton meters (joules for energy).
Torque = mass of the door * acceleration * lever arm * sine angle of force applied
The length of the lever arm depends on where you push the door. If you assume the acceleration is proportionately greater the shorter the lever arm, you get the same torque and thus the same energy transferred to the door. Depending on your assumptions, the amount of energy transferred to the door needn't differ from pushing it near its edge.
Assuming an ordinary hinged door ($M = 3Kg$, L = 1m), would it take more energy to open it when applying force in the middle of the door (point b: $r=50cm$), rather than at the end of the door (point a $r=100cm$), My own answer is no, since the change in force would be proportional to the distance required to open the door and therefore the total energy would remain the same.
The issue is not so simple: the equation $E = F*d= F_1*r_1 = F_2*r_2$ is valid only with a lever, where forces are balanced across the fulcrum F. (left sketch)
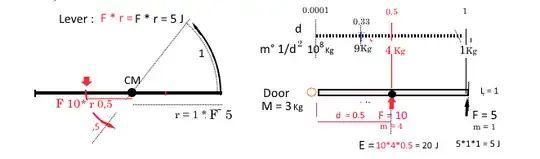
In a door, the center of mass is not at the fulcrum, but at half-length, and the effective mass $m°$of the door varies between $M/3$ (at tip) to $\infty$ (at fulcrum), according to the formula of the rotational mass divided by the square of the distance from the fulcrum/hinge (right diagram): $$m° = \frac{[M]=3*l^2=[1]}{3*d^2}= \frac{1}{d^2}$$
Therefore the nearest to the hinge you are applying the force/impulse, the more energy is required to obtain the same result (the same change of momentum), because the effective rotational mass increases as you get near the fulcrum. In a lever, the mass of the arm is not considered as it is constant, on a hinge, the energy required to displace the door at point $b$ is roughly proportional to the increased mass $E = m*a*d$. I said roughly, because applying a force/torque to a pivoted object is more complex than it may seem, because you have to distinguish between fixed load and follower load. But, grossly simplifying, we may say that it takes a lot more energy at point $b$. Friction and wasted energy are just red herrings
If at first you find this hard to believe, just think that if you apply any force bang to the hinge, no matter how great, the door won't budge. (Unless you bring down the wall, of course). Now, this change of result can't be abrupt, must increase gradually, an it does, by the inverse square law.
What about the situation where you forcefully push the door open ( $J=10kgm/s$), rather than pushing it with the same acceleration throughtout the whole movement? – JonathanReez
! Considering an impulse $J$ (any force must be applied for a time, every force is an impulse) greatly simplifies your calcs. Even though the results are some what different, the principle, is un-changed.
Same for the idea that the change in the door's position can't be abrupt as you move the point of application of the force from the hinge further out. The door won't move if you push at the hinge; it will move if you push elsewhere. That is an abrupt change. . – David Z♦
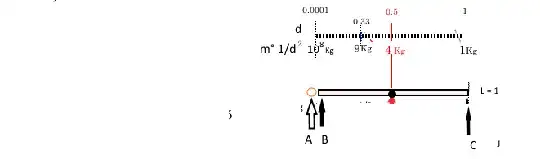
Practically you are affirming that: if you give K J of energy (the question was about energy so we must always condider that) at point A, the door will not move, then, if you apply same force at 0.0001 m from the hinge (B) or at 1 m distance (C) .the door will move with same angular velocity/momentum/energy.
If that is what you meant, it needs no comment.
I am ready to admit this post is incorrect, if someone shows a (any) concrete example (with real figures) of same force applied at B and C with same result.
