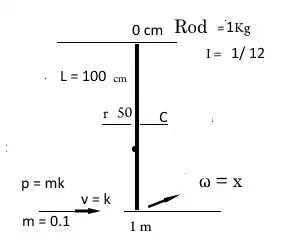
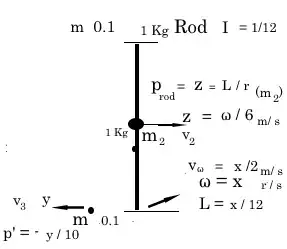
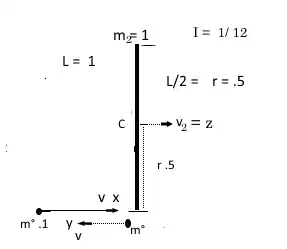
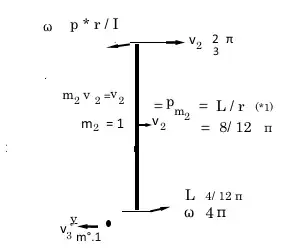
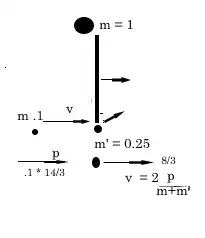
A 1 meter long rod on the ice with mass $m_2=1$ kg is perpendicularly hit on one end by a point particle with mass $m_1=0.1$ kg. The collision is elastic and the point particle is bounced back in the same direction. After the collision the rod's frequency is $\nu =2$ Hz. What was the initial velocity of the point particle?
My attempt:
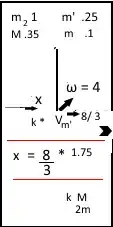
Since the collision is elastic, the kinetic energy of the system is the same before and after the collision: $$0.5m_1v_1^2=0.5J_2 \omega_2^2+0.5m_2v_2^2+0.5m_1v_3^2$$ Where $v_3$ is the velocity of the point particle after the collision.
Now, in the case of a rod: $$J=\frac{1}{12}L^2m$$ And, we also know: $$\omega_2=2 \pi \nu$$ And there are also no external forces, therefor the momentum of the system is the same before and after the collision: $$m_1\vec{v_1}=m_1 \vec{v_3}+m_2\vec{v_2}$$ Here $v_1$ is the quantity we're looking for, $v_3$ is the point particle's velocity after the collision and $v_2$ is the velocity of the rod's center of mass. It follows: $$\vec{v_2}=\frac{m_1 \vec{v_1}-m_1 \vec{v_3}}{m_2}$$ From this it follows: $$0.5m_1v_1^2=\frac{1}{24}L^2m_2 4 \pi^2 \nu^2+0.5m_2 \left|\frac{m_1 \vec{v_1}-m_1 \vec{v_3}}{m_2}\right|^2+m_1v_3^2$$ This is 1 equation with 2 unknowns, and this is where I get stuck. Any help is appreciated.
 Using conservation of energy:
Using conservation of energy: