In his book, the author says that according to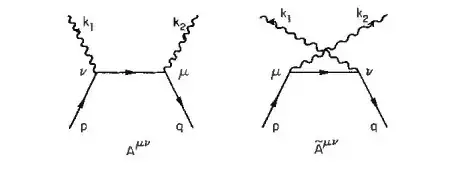 
the Feynman diagrams of this process in QED $$e^+ e^- \rightarrow \gamma \gamma,$$ gauge invariance requires that $$k_{1\nu}(A^{\mu\nu} + \tilde{A}^{\mu\nu})=0=k_{2\mu}(A^{\mu\nu} + \tilde{A}^{\mu\nu}).$$ My question is how does gauge invariance set this statement equal to zero?
The amplitude for emission of n photons with polarizations $\epsilon_{\mu_j}$ written as $\epsilon_{\mu_1}\ldots \epsilon_{\mu_n}\mathcal{M}^{\mu_1 \ldots \mu_n}$ satisfies $k_{\mu_1} \mathcal{M}^{\mu_1 \ldots \mu_n} = k_{\mu_2} \mathcal{M}^{\mu_1 \ldots \mu_n} = \ldots =0$ due to gauge invariance (do you know this fact? This is a consequence of ward identity & abelian gauge symmetry)
For your process of two photon emission $\mathcal{M}^{\mu_1 \mu_2}\equiv A^{\mu_1 \mu_2}+\tilde{A}^{\mu_1 \mu_2}$. So it should become clear
