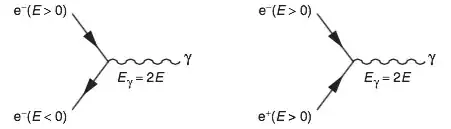Feynman-Stueckelberg interpretation

Question

My question is related to the interpretation of antiparticles. According to the so called Feynman-Stueckelberg interpretation a negative energy solution of the Dirac equation corresponds to a positron which then runs apparently backwards in time. But if I consider the vertex of a electron-positron annihilation I have at this vertex an incoming electron with positive energy which under "emission" of a virtual photon turns into a (the vertex) leaving positron which runs backwards in time. But this way several conservation laws seem to be violated.

I would in fact expect the positron not to leave the vertex but entering the vertex. In that case the conservation laws would be fulfilled.

However, for me a solution of ~exp(iEt) is either a negative energy electron running forwards in time or a positive energy positron running backwards in time. But I cannot fit that with the electron-positron annihilation (see above). I would be grateful if somebody could dissipate by confusion.

Answer 1

A negative energy particle running backwards in time is mathematically equivalent to a positive energy antiparticle running forwards in time.

Since the time dependence of the wavefunction is of the form $exp[-iEt]$ for particles that run forward in time, then the simultaneous transformation $t \to -t$ and $E \to -E$ will give you:

$$ exp[-i(-E)(-t) \equiv exp[-iEt]$$

i.e the time dependence is unchanged. Hence the two pictures are mathematically indistinguishable.

Lets illustrate this with an example. Consider the two vertices below:

I claimed before that these 2 vertices are mathematically equivalent. How so? Well, in the left diagram, a positive energy electron emits a photon of energy 2E, and in order to conserve energy, a negative energy electron is emitted propagating backwards in time (from the solutions of the Dirac equation).

This is equivalent to the second diagram because you can interpret it like this: The positive energy electron is annihilating with the positive energy positron (both here propagating forwards in time) and in order to conserve energy they produce a photon of energy 2E.

For further reading I suggest the book Modern Particle Physics by Mark Thompson

Answer 2

According to the so called Feynman-Stueckelberg interpretation a negative energy solution of the Dirac equation corresponds to a positron which then runs apparently backwards in time.

A negative energy solution corresponds to an electron running backwards in time, which is the same thing as a positron running forwards in time.

A positron runnning backwards in time would be an electron.

To be a bit more explicit:

Say we have an equation that describes particles with negative charge. While analyzing its implications, we find that it requires solutions with negative energy $p_0 < 0$, ie the particle's momentum points in the direction opposite to coordinate time!

Because time travel is a Bad Thing as far as physicists are concerned, we have to discard our equation or try to 'argue away' its problems.

So let's assume such particles did indeed exists. How would they manifest, eg what would their trajectories look like in a magnetic field? Well, they would essentially look like an ordinary particle with opposite (thus positive) charge!

So we reinterpret a particle with negative energy (ie having momentum pointing towards the past) as an anti-particle with positive energy.