63

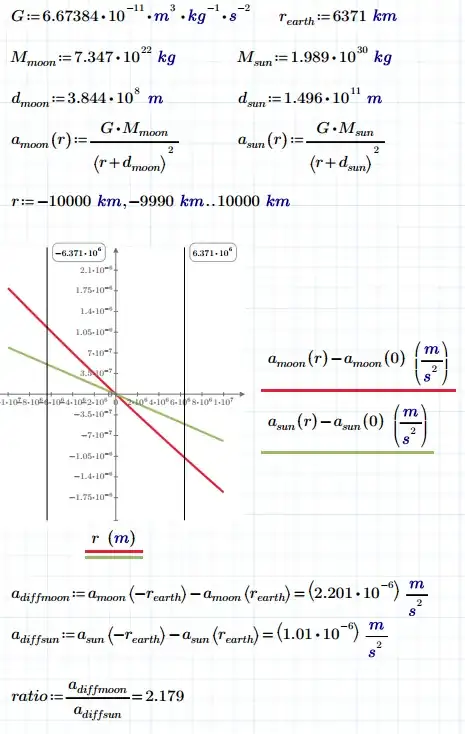
You have likely read in books that tides are mainly caused by the Moon. When the Moon is high in the sky, it pulls the water on the Earth upward and a high-tide happens. There is some similar effect causing low-tides. They also say that the Sun does the same as well, but has smaller effect compared to the Moon.

Here's my question: Why is the Moon the major cause of tides? Why not the Sun? The Sun is extremely massive compared to the Moon. One might say, well, the Sun is much farther than the Moon. But I've got a simple answer: Just substitute those numbers in $a=\frac{GM}{d^2}$ and find gravitational acceleration for the Moon and then for the Sun (on Earth, by the way). You'll find something around $3.38$ $10^{-6}$ $g$ for the Moon and $6.05$ $10^{-4}$ $g$ for the Sun - I double checked it to make sure. As you can see, the sun pulls about $180$ times stronger on the Earth. Can anyone explain this? Thanks is advance.

Moctava Farzán
  • 1,924

5 Answers5

83

What is important for tidal forces is not the absolute gravity, but the differential gravity across the planet, that is, how different is the force of gravity at a point on the Earth's surface near the sun relative to a point on the Earth's surface far from the sun. If you compare it with the moon, the result will be that the tidal force from the sun is about 0.43 that of the moon.

Suppose two different bodies in the sky that have the same apparent size. Because the mass M of the object will grow as $r^3$ (because $M=4/3\rho\pi R^3$ and $R=\theta r$), the gravitational force will actually grow linearly with $r$, where $r$ is the distance and $R$ is the radius of the object. So if two bodies have the same apparent size (such as the Moon and the Sun) and the same density, the tidal force would be the same. The density of the moon is about 2.3 times larger than that of the sun, that is why the tidal force is larger by that factor.

43

Tides are caused by the gradient of the gravitational field - so the tidal "force" experienced drops with the third power of the distance.

This means that the relative strength of the tides should go as

\begin{align} \mathrm{ratio} & = \frac{M_\mathrm{moon} \cdot D_\mathrm{sun}^3}{M_\mathrm{sun} \cdot D_\mathrm{moon}^3} \\ & = \frac{7 \cdot 10^{22}\cdot (1.5 \cdot 10^{11})^3}{2\cdot 10^{30}\cdot (3.7\cdot 10^{8})^3} \\ & = 2.3 \end{align}

So although the sun is more massive, its greater distance makes its tidal force about 2.3x weaker than the moon's - consistent with your number (and my round numbers...)

Following a suggestion by @wolprhram jonny, if you assume a certain angular size $\alpha$ of the sun/moon (they are both about 0.5° across as seen from Earth), you can rewrite the above equation by first replacing mass with density times volume, then rearranging: \begin{align} \mathrm{ratio} & = \frac{(\rho_\mathrm{moon}r_\mathrm{moon}^3)\cdot D_\mathrm{sun}^3}{ (\rho_\mathrm{sun} r_\mathrm{sun}^3)\cdot D_\mathrm{moon}^3} \\ & = \frac{\rho_\mathrm{moon}\alpha_\mathrm{moon}^3}{ \rho_\mathrm{sum} \alpha_\mathrm{sun}^3} \end{align}

So when the apparent angle in the sky is the same, the tidal forces scale with the density of the objects. Interesting and unexpected result.

Emilio Pisanty
  • 137,480
Floris
  • 119,981
12

The highly upvoted answer is right but to make things much simpler:

Tides are based on the change in gravity, not the gravity. That means they drop off at the cube of the distance rather than the square of the distance like gravity itself does. Thus the object with the most gravity isn't necessarily the one that causes the most tide.

Loren Pechtel
  • 1,739
10

As stated in other answers it is how much the gravitational force is different by on opposite sides of the earth that creates the tides.

You can still show this using $a=\frac{GM}{d^2}$ but you need to consider the difference, not the absolute force on the earth.

The sun while much more massive is just far enough away that it is getting to a much flatter part of the hyperbola.

Everything is better with graphs

Maths and Graphs

Hugoagogo
  • 250
-3

Behind any theory, the field reality indicate a stronger lunar tide for:

-oceanic waters (the lunar influence is detected as M2 and K1 tidal components; the tidal component is defined by the frequency of a tidal oscillation; the frequency is dependent on the relative movement of the implied celestial bodies (Eartth, Moon/Sun).

-earth's crust (the same tidal components; the tidal response is no longer influenced by coastal morphologies, but by the local mass change caused by oceanic loading and crustal deformation induced by oceanic loading) http://en.wikipedia.org/wiki/Earth_tide

-inland groundwater and rivers (the description "inland" was used because the coastal groundwater and rivers are influenced by the oceanic input; the K1 and M2 are much weaker when compared to their oceanic equivalents vecause many other strong cycles interfere, such as the day/night cycle) http://www.nature.com/srep/2014/140226/srep04193/full/srep04193.html

Andrei
  • 1