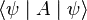I read a book on pop sci book on quantum mechanics and the author said that electrons do not fall into the nucleus due to quantum mechanics- which principles suggest this (I think it was Heisenberg's Uncertainty and Pauli's Exclusion Principle) and why?
Also, I've heard that if Bohr's planetary model were correct, then electrons would lose energy/momentum and fall in- is this true and again, which physics principles say this?
I read a book on pop sci book on quantum mechanics and the author said that electrons do not fall into the nucleus due to quantum mechanics- which principles suggest this (I think it was Heisenberg's Uncertainty and Pauli's Exclusion Principle) and why?
The basic argument can be based on two things from non-relativistic Schroedinger theory:
1) for common Hamiltonians for the atom (like the one Schroedinger used for hydrogen atom) there is a $\psi_0$ function for which the average expected energy defined as $$ \int \psi_0^* \hat{H}\psi_0\,dq $$ is lowest possible;
2) the atom won't go spontaneously into state where the associated $\psi$ function would give average expected energy $$ \int \psi^* \hat{H}\psi\,dq $$ higher than that. As $\psi_0$ has characteristic dimension of Bohr radius $10^{-10}~$m, there is no collapse; more concentrated function would give higher average energy.
Also, I've heard that if Bohr's planetary model were correct, then electrons would lose energy/momentum and fall in- is this true and again, which physics principles say this?
That is incorrect. Bohr's model as opposed to previous electromagnetic models (Thomson's or Rutherford's) states explicitly new assumption, that there are stable orbits where atom does not lose energy by radiation - it has an exemption on those orbits. The problem with the radiation of energy was stressed by Bohr when formulating his model as unsatisfactory feature of the older electromagnetic models.
Please keep in mind that physics does not answer "why" questions on the very basic observations that generated the need for a theory/mathematical model. Your question touches on one of the basic reasons that quantum mechanics was developed as a theory of the microcosm, and thus its only answer is really "because that is what we have observed".
I read a book on pop sci book on quantum mechanics and the author said that electrons do not fall into the nucleus due to quantum mechanics- which principles suggest this (I think it was Heisenberg's Uncertainty and Pauli's Exclusion Principle) and why?
It is a basic experimental observation that at the energies we live in atoms exist. It is also a basic observation that they are composed by a nucleus and electrons around them. The simplest is the hydrogen atom.
According to classical electrodynamics developed in the nineteenth century, which btw has been a very successful theory, a charge going in circular or elliptical orbits around an opposite charge should radiate away its kinetic energy because of the angular acceleration into electromagnetic radiation , continuously, until it falls on the nucleus. The spectrum should be continuous.
What did the data say? An electron around a hydrogen atom, for simplicity, could be at a high energy "orbit" but the radiation as it was falling down into the proton(nucleus) was not continuous but composed of quanta, photons, what we have classified by now as elementary particles. Photons were known by the photo electric effect , but that is another story.
This leads us to the Bohr planetary model:
Also, I've heard that if Bohr's planetary model were correct, then electrons would lose energy/momentum and fall in- is this true and again, which physics principles say this?
which imposed quantized orbits, i.e. orbits with specific energies to explain by the transitions to lower states the quantized nature of the fall into the nucleus and the fact that there existed a ground state. It was an ad hoc postulate of a whole model in order to explain the observations.
This imposed the need for a formal theory to explain the observations with a few postulates and a mathematical structure, i.e. the development of quantum mechanics, which includes
Heisenberg's Uncertainty and Pauli's Exclusion Principle
in the framework
As QM mechanics is a self consistent theory which predicts new phenomena successfully every time, one can start with one set of assumptions and say they explain another set of assumptions, but the truth is that the postulates are the place where the real world observations are imposed on the mathematical framework, in this case
Physical observables are represented by Hermitian matrices on H.
The expectation value (in the sense of probability theory) of the observable A for the system in state represented by the unit vector |ψ⟩ ∈ H is
By spectral theory, we can associate a probability measure to the values of A in any state ψ. We can also show that the possible values of the observable A in any state must belong to the spectrum of A. In the special case A has only discrete spectrum, the possible outcomes of measuring A are its eigenvalues
Any "why" hittng on the postulates can have only the answer "because that is what we have observed and modeled" .
Of course the electron can "fall" into nucleus. In neutron stars this happens.
The question is why the atoms stable in our surroundings. The classical physics can't give an answer because the permanent electrons acceleration during his circular move around the nucleus would have to be accompanied by radiation and the loss of speed. But this does not happens. So there were found rules which describe the explored electron orbitals and approve this rules by predicting the orbitals for new orbitals.
The QM has circumnavigate around this phenomena by using statistical methods that describe this phenomena but not explain the reasons. This method succesful - more than classical physics - predict more complicated atom states.
What we know until now is that the gravitational, the strong nuclear and the weak nuclear forces are not responsible. What we know else is that the electrostatic force does not work nearby the nucleus. The interaction between the positive and the negative charged particles stops at some distance. The reason is not found and so your question remains open.
This can be explained using Bohr's model of the hydrogen atom, de Broglie's wavelength and simple algebra and geometry.
De Broglie's wavelength comes from Einstein's equation for the energy of a particle $E=\sqrt{\rho^2c^2 + m_0^2c^4}$, where $\rho$ is the momentum of the particle, $m_0$ is its rest mass and $c$ is the speed of light. This equation already relates mass with light, but de Broglie takes it a step further.
Light has no rest mass, so for a photon $m_0 = 0$. The energy of a photon is proportional to its frequency $f$ and described by the equation $E=hf$, where $h$ is Plank's constant. Because the speed of a wave is the product of its wavelength $\lambda$ and frequency (waves per second), the energy of a photon can be rewritten as $E=\frac{hc}{\lambda}$. Plugging these terms into Einstein's equation produces $\frac{hc}{\lambda}=\rho c \implies\lambda=\frac{h}{\rho}$. This is de Broglie's wavelength, in which $\rho=\frac{h}{\lambda}$ for the momentum of a photon, and $\rho=mv$ for the momentum of a particle.
The equation describes the matter-wave and can be used to determine the wavelength of any particle that has momentum.
Now, using Bohr's model, let's compute the wavelength of an electron in a ground state hydrogen atom, orbiting the nucleus at the Bohr radius denoted by $a$. We can find the electron's speed by replacing the centripetal force with Coulomb's law and then plugging it into de Broglie's wavelength:
$F_c=m\frac{v^2}{R}\implies F_E=m_e\frac{v_e^2}{a}\implies \frac{1}{4\pi\epsilon_0}\frac{e^2}{a^2}=m_e\frac{v_e^2}{a}\implies v_e=\frac{1}{2}\frac{e}{\sqrt{am_e\pi\epsilon_0}}\implies \lambda_e=2\frac{h}{e}\sqrt{\frac{a\pi\epsilon_0}{m_e}}$
Which gives an electron wave with $\lambda_e=0.33$nm
Because the circumference of a circle is $C=2\pi r$, we can find the number $n$ of wavelengths that the electron wave has around the Bohr radius:
$n=2\frac{\pi a}{\lambda_e}=1$
This describes a circular, standing electron wave that is oscillating around the nucleus at the Bohr radius. Because only one wavelength fits around the circumference of this orbit, it represents the smallest possible orbit for the electron wave, which is at n=1.
Now, for fun, let's compute the proton's wavelength. Since the proton is more massive, we should expect its wavelength to be much smaller. Because we are using classical mechanics, it is appropriate to define a center of mass, denoted by $r_{cm}$, between the proton and electron. Once this is done, the velocity of the proton around this center can be found and plugged into de Broglie's wavelength:
$r_{cm}=\frac{m_ea}{m_p+m_e}\implies \frac{1}{4\pi\epsilon_0}\frac{e^2}{a^2}=\frac{m_p(m_p+m_e)v_p^2}{m_ea}\implies v_p=\frac{1}{2}e\sqrt{\frac{1}{a\pi\epsilon_0}\frac{m_e}{m_p(m_p+m_e)}}$$\implies\lambda_p=2\frac{h}{e}\sqrt{{a\pi\epsilon_0}\frac{m_p+m_e}{m_pm_e}}$
$\lambda_p=0.010$nm
Let's compute how many wavelengths can fit into this radius:
$n=2\frac{\pi r_{cm}}{\lambda_p}=0$
The proton can not exist as a standing, circular wave. The radius $r_{cm}$ is about $\frac{1}{1000}$ times the wavelength $\lambda_p$. Compared to the Bohr radius, the proton is also significantly small. For these reasons it is sufficient to take the proton as a point mass, in this model.
In conclusion, the electron, as a standing wave, can only exist at certain radii in the atom, in which $n=\frac{2\pi r}{\lambda}$ is equal to a whole number $≥1$. At the Bohr radius in the hydrogen atom, $n=1$. Therefore, the wave will destabilize if brought any closer to the proton by deconstructive interference. The Bohr radius is the closest the electron wave can approach the proton. Furthermore, if we tried to increase the electron's frequency and number of waves, in order to force it closer to the nucleus, it would require an enormous amount of energy, because we would have to condense the wave to a single point.
This, of course, is a model and should not be taken as a real phenomenon.
there is an explanation from quantum field theory point of view.we can calculate amplitudes for free electron and proton to bound state situation of hydrogen atom. there is finite amplitude for this process. and there are also finite amplitude for the process of bound state of electron and proton(hydrogen atom) to photons. we can calculate decay rate for this process. then we will see that from how much time this will happen. this is different from our normal scattering amplitudes in which particles are well separated in the distant past and distant future.
It does.
Refer Electron Capture and related scientific literature.
Edit1: I guess the question does not ask about this specific process but about the foundations of quantum mechanics. The stability of the atom is an old problem. If an electron is treated classically, then it would fall into atom, due to radiation emitted by accelerating particles. It has been observed that atoms are stable(Not the kind that the electron capture refers to) Posulates of quantum mechanics explain precisely explain that stability. You will find the details in any text book. And Please read text books not pop sci books. It would be more helpful.
Edit2: Basically the central Postulate of quantum mechanics is [x,p] = i. I can go on and explain it to you, as far as I understand. but Really it would be best if you tried to understand it and then if you are stuck then we can discuss it.
Do read Bohr's articles they are rather insightful.
rmhleo points out above that in some kinds of radioactive decay, electrons are captured by the decaying nucleus. So presumably electrons do commonly fall into the nucleus -- but usually they fall back out again rather than staying there.
The following is only a way to imagine it which as far as I know cannot be experimentally tested:
Imagine two electrons in circular orbit around a nucleus. They do not radiate to the world because radiation is perpendicular to the direction of motion, and they cancel each other's waves.
Because of the lightspeed delay, each of them appears to the other to be behind in the orbit, so each of them provides a repulsive force that tends to slow them. This is not the electric force, which appears to come from the direction that each electron would have been if it traveled in a straight line at its previous velocity. But the radiative force is offcenter. At different speeds the force has different intensities, from different distances and directions.
So paired electrons are more stable than single ones.
I find it a pleasant picture, but it isn't QM and we can't actually measure those orbits.
