Why doesn't an electron ever hit (and stick on) a proton?

Question

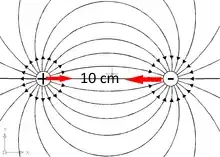
Imagine there is a proton confined in a box and we put an electron at 10 cm distance:

It gets an acceleration of thousands of meters/second^2 along a straight line joining the two CM's.

One would expect the electron to hit the positive particle in a fraction of a second, and stick there glued by a huge force, but this does not happen, even if we shoot the electron providing extra KE and velocity/momentum.

Is there a plausible explanation for that? Why doesn't the electron follow the straight force line that leads to the proton?

Edit

my question has been misunderstood: is not about orbitals or collisions. If it has an answer/explanation it is irrelevant if it refers to classical or QM physics. No explanation has been presented.

• We know that a) two protons can stick together even though repel each other via Coulomb force, it is legitimate then, a fortiori, to suppose that b) two particles that do not repel each other can comfortably sit side by side, almost touching each other:

2a) proton proton

2b) proton electron

• we also know that in a TV tube electrons leave the guns and hit the screen following incredibly precise trajectories producing pictures in spite of HUP and the fact the are a

"... a point particle having no size or position"

Now the situation I envisaged is very simple, and probably can be adequately answered step by step with yes/no or (approximate) figures:

• 0) When the electron is in the gun/box is it a point-mass/charge or is it a probability wave smeared over a region. when it hits the screen doess it have a definite size/position?
• 1) does electrostatics and Coulomb law apply here? do we know with tolerable precision what acceleration the electron will get when it is released and what KE and velocity it will aquire whenit ges near the proton?
• 2) if we repeat the experiment billion of times can those figures change?
• 3) according to electrostatics the electron should follow the force line of the electric field leatding to the CM of the proton and, when it gets there, remain as near as possible glued by an incredibly huge Coulomb force (picture 2 b). This does not happen,....never, not even by a remote probability chance. What happens, what prevents this from happening? Physics says that only a very strong force can alter the outcome of other laws.An answers states that QM has solved this long-standing mystery but does not give the solution.

Answer 1

The electron and proton aren't like pool balls. The electron is normally considered to be pointlike, i.e. has no size, but what this really means is that any apparent size we measure is a function of our probe energy and as we take the probe energy to infinity the measured size falls without limit. The proton has a size (about 1fm) but only because it's made up of three pointlike quarks - the size is actually just the size of the quark orbits and the proton isn't solid.

Classically two pointlike particles, an electron and a quark, can never collide because if they're pointlike their frontal area is zero and you can't hit a target that has a zero area.

What actually happens is that the electron and quark are quantum objects that don't have a position or a size. They are both described by some probability distribution. Quantum mechanics tells us that a reaction between the electron and quark can occur, and indeed this is what happens when you collide particles in an accelerator like the LHC. However in your experiment the colliding electron and proton don't have enough energy to create new particles, so they are doomed to just oscillate around each other indefinitely.

If you accelerate the electron you can give it enough energy for a reaction to occur. This process is known as deep inelastic scattering and historically this experiment has been an important way we've learned about the structure of protons.

Answer 2

This was a big mystery before quantum mechanics was discovered. Not only are electrons attracted to protons, electrons radiate away energy when accelerated. A classical electron in orbit around a proton should spiral into the nucleus in a small fraction of a second.

The "explanation" is that classical physics doesn't work on a small scale. Quantum mechanics is a better model. It isn't a reason why. It is just a description of how the world is. It isn't always intuitive or plausible.

In quantum mechanics, an electron doesn't have a definite position or momentum. It has a wave function from which the probability of finding it at a particular position or momentum can be calculated. An electron bound to a proton will probably be very near the proton.

The Uncertainty Principle says that if the uncertainty of an electron's position is reduced by confining near a proton, then the uncertainty in its momentum increases. An electron that may have a high momentum isn't likely to stay near a proton very long.

There is a size where these two opposing uncertainties balance. This determines the size of atoms.

This was a very loose, hand-waving description. If you want the real story, there is a lot on the web. Volume III of The Feynman Lectures is a good introduction.

Answer 3

This type of model, a classical model, led to the Bohr model and quantum mechanics for the atom, as it is an experimental fact that the Hydrogen atom exists and does not turn into a neutron.

For the large distances you illustrate the classical trajectory would have to be exactly centered otherwise, even classically there will be lateral motion that will create a hyperbolic orbit.In the quantum mechanical framework which is the correct one when discussing elementary particles, exact lines do not exist, the position and energy are bounded by the Heisenberg uncertainty principle , and the electron and the proton are in the quantum mechanical regime, so the probability of a lateral motion is very high.

In the center of mass system, electrons and protons are attracted the way you describe in the figure. Electron proton scattering, which is what you are describing, has been studied and if the energy of the electron is high enough it will scatter off the field of the proton. If it is lower than the hydrogen lines, it will be caught by the fields into a hydrogen atom, emitting the appropriate energy as a photon.

Quantum mechanics does not allow "mergings" in the way you envisage them. There exists electron capture in nuclei, a proton capturing an electron and becoming a neutron, but again this is a specific quantum mechanical solution within the nucleus.

Answer 4

The answer to your revised question is that your object 2b does exist, is correctly described as an electron stuck to a proton via Coulomb attraction, and is what you get (most of the time) if you take a single electron and a single proton and place them in an otherwise empty universe, initially at rest in the center-of-mass frame. The initial separation distance only affects how long it takes for the electron to become stuck and how much energy is released in the process. The object is generally known as a hydrogen atom.

This sentence is accurate:

(3) according to electrostatics the electron should follow the force line of the electric field leading to the CM of the proton and, when it gets there, remain as near as possible glued by an incredibly huge Coulomb force (picture 2 b).

That is exactly what happens. (The excess energy will be released as photons.) You think it doesn't happen, and I'm not sure why. My best guess is that you are clinging to the inaccurate "Bohr model" of a hydrogen atom, in which the electron "orbits" the proton at a distance. That model was scrapped because there was no plausible reason why the electron should remain at a distance from the proton.

Now, there is an important detail, which is that the electron in a hydrogen atom is still moving, even though it is stuck to the proton, and it does get some distance away from the proton from time to time (but it is most likely to be very close to, or even inside, the proton, unless you hit the atom with a photon or two and "excite" the electron). This is the point where you have to bring in just a little bit of quantum theory (indeed, it is one of the first phenomena that quantum theory was invented to explain). Quantum theory proposes that nothing can ever completely stop moving. This is one way to express the famous uncertainty principle, and I think it's the clearest way to put it in the context of this particular phenomenon.

Okay, why can nothing ever completely stop moving? Because everything is a wave, and waves only exist when they are in motion. I could elaborate on that statement, but only by throwing a bunch of math at you, and I don't think that will help. (The linked article on the uncertainty principle goes into the math.)

Answer 5

The diagrams in the question shouldn't be taken literally. As Matt Strassler explains it is wrong to think of the proton as just having 3 quarks. Instead, there is a vast multitude of quarks and antiquarks, without being able to distinguish real from virtual.

We know that a) two protons can stick together

That would be a diproton which isn't stable. So, no, two protons can't stick together without at least one neutron. Also, the protons can interact with each other through the residual strong force, while a proton and electron can not.

According to Proton Structure from the Measurement of 2S-2P Transition Frequencies of Muonic Hydrogen Science Vol. 339, pp. 417-420:

...the comparison between theory and experiment has been hampered by the lack of accurate knowledge of the proton charge and magnetization distributions. The proton structure is important because an electron in an S state has a nonzero probability to be inside the proton. The attractive force between the proton and the electron is thereby reduced because the electric field inside the charge distribution is smaller than the corresponding field produced by a point charge.

The electron can be within the proton. This is the Fermi Contact Interaction. The Fermi contact interaction is observable through NMR, EPR and electron capture. The electron does not become trapped within the proton, because the proton does not constitute an infinite well. Inside the proton is the most probable location (for a given small volume) for the electron to be in the hydrogen ground state, but it is not the only location because the proton is not an infinitely deep potential energy well.

For a quantitative model of the actual charge distribution in the proton see Proton form-factor dependence of the finite-size correction to the Lamb shift in muonic hydrogen

•1) does electrostatics and Coulomb law apply here?

Coulomb's law does not apply exactly. It needs to be replaced by quantum electrodynamics.

Answer 6

While this is a lie we tell to children, one way to understand what is going on is Heisenberg Uncertainty.

The product of the certainty of location and the certainty of velocity is bounded below.

This means that as the volume of where something is confined to grows, its velocity has to grow.

You can work out how strong the attraction is between a proton and an electron. If the electron has more kinetic energy than this, the attraction between the proton and the electron won't be strong enough to keep it confined.

So the attraction between the proton and electron determines how small the region the electron can be confined in is.

A "collision" requires that the electron and proton both be at the "same" small location. What happens then? Well, if they don't have enough energy to spawn new particles, they just fly apart. If they do have enough energy to spawn new particles, they do sometimes, and they stop being a proton and an electron. Bang, they hit each other.

But without enough energy to form new particles, the electron instead forms a "cloud" of states around the proton, where the radius of the cloud is determined by the binding energy between the proton and electron.

Of interest is what happens when you add more electrons and protons (presuming you manage to keep the protons together): the Pauli exclusion principle kicks in, and the new electrons have to "stack up" on top of the old ones in the "closer" states.

Now, how do the protons stick together? With the help of neutrons, the nuclear forces provide a much stronger binding energy. This results in them being confined to a smaller radius (the nucleus) than the electron orbitals.

Answer 7

There are two important aspects of an electron that must be kept in mind: 1) at "low" velocities, it acts like a particle (Classical physics applies). 2) at "atomic scale," it acts like a wave (QM applies).

Answers to your questions:

0) Since low velocity is involved, the electron acts like a point particle. When it hits the screen, it does have a definite size and position.

1) Yes, electrostatics and Coulomb's law apply, but because the electron is in motion, other laws also apply (Ampere's, Faraday's, etc.).

2) Repeating the experiment billions of times would be equivalent to using many electrons at the same time (a current), which is exactly what is used in an "electron gun." Since a large group of electrons is used, the results become more precise/predictable, allowing the use of "Classical" physics.

3) As mentioned in 1), electrostatics and Coulomb's law are not sufficient to explain the electron's motion. Because of self-induction, as the electron moves towards the proton, a force perpendicular to both the velocity vector and the line connecting the electron and proton (tangential to proton), is generated/induced. As the separation is reduced, the induced tangential force increases causing a larger and larger tangential velocity. At the same time, the normal acceleration due to Coulomb's law, also increases. At some point, both the centrifugal acceleration (due to the tangential velocity) and the normal acceleration will be equal and opposite each other, so the electron will "circle" the proton (at the Bohr radius) and thus, a hydrogen atom is created.

For an electron with higher energies, appropriate answers have already been provided.

Answer 8

You've got a lot of explanations and I want to add one more.

Interaction of fields by one-dimensional structures in space

Years ago I worked about One-dimensional structures of space and somehow applied the results to electric fields, magnetic fields and EM radiation and it came out that only two types of quanta are needed to describe them all. So the description of fields through field lines get a materialistic base, with this two quanta and clusters of them it is possible to describe the electric as well as the magnetic field and also photons.

Quantized character of the interaction

During the approach of an electron and a proton the field lines get shorter but due the an assumption in my eleboration the clusters have to follow a continuous function and the number of quanta in them should increase with a constant number. So some of the quanta get emitted as photons and some of them at the ands of the "chain" go over to the proton and the electron. At some distance between them it isn't more possible to shorten the field lines, the emission of photons stops and the transition of quanta to inside the proton and the electron stops too.

My paper is very dry written and the translation to the English language does it not make better but it has really new ideas and until now no one inconsistency.