I will attempt to go more in-depth into the physics here. In practice, the unloaded weight of the car is non-zero, but I'll consider two states where the first state refers to zero weight on the tire. In order to make a practical calculation for the car, then, you'll use the numbers for the second state, subtracting one vehicle weight from another.
There are two governing equations that I see playing out, and these have been laid out by other answers, although not in so-many variables. Again, I'll use "state 1" to denote no loading and "state 2" the loaded state.
$$ P_1 V_1 = P_2 V_2 $$
A note about justification: this assumes the temperature is set. There is an infinite temperature sink available in the form of the ambient environment. So you'll have some temperature change if you load a vehicle quickly, but over time the tire temperature is dictated entirely by operating conditions. Moving on to the second equation I have in mind, we equate the footprint and the pressure on that footprint to the weight being supported. I'm assuming the tire has no weight.
$$ A_{ft,2} P_2 = M g $$
For state 1, this is trivial equation, so I do not write it. The A, area, here is the footprint area. This is different from the total geometric tire area. This is only the area of contact between the tire and the ground. I'll have to neglect any contributions from the rigidity of the tire itself.
It would be a straightforward matter to equate the footprint area of a torus to the remaining volume above-ground. However, the torus equation is complicated. I'll assume a spherical tire. This is still more detailed than any other attempt so-far, although the door is open if someone wants to do more work.
$$ A_{ft} = \frac{M g }{ P} = \pi \left( R^2 - (h-R)^2 \right) = \pi ( 2 R h - h^2 ) \\
V = \int_{h-R}^{R} \pi \left( R^2 - z^2 \right) dz = \left[ z R^2 - \frac{1}{3} z^3 \right]_{h-R}^{R} \\
= \pi \left( \frac{4}{3} R^3 - h^2 ( R - \frac{1}{3} h ) \right) $$
To apply this, for the unloaded state observe that h=0. For the loaded state, the first equation above can be solved for the height displacement. We will imagine that we know the unloaded tire pressure, so everything in that equation is solved for. Now we can return to the P1 V1 = P2 V2 equation, and solve for P2. The V1 term is simply the volume of a perfect sphere. Then, we have V2 in terms of h, and we have h in terms of P2. This yields an equation that you can solve for P2, but it's a high order polynomial.
Here are some numbers, which vaguely represent a Corolla.
- P1 = 30 psi = 206842.7 Pa
- R = 28.85/2 inches = 0.3155 meters
Plugging these in, we can solve it numerically. However, in doing this, we need to correct for the egregious assumption of a spherical tire, as well as account for the 4 wheels. A typical tire volume is on the order of 10 L, and the sphere in my case is 131.5 L. So for realism, I'm correcting the loading by the ratio between these two, 131.5 L to 40 L.
With that, here are the numbers I get. This is the pressure in Pa versus the car loading in Newtons.
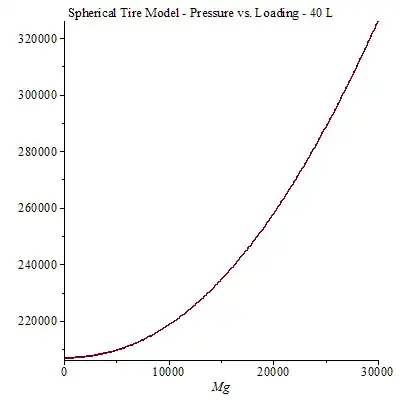
EDIT: This is the corrected, second version of the graph. It still uses all the above parameters, but take note this assumes 40 L tire total volume. I had missed a factor of pi.
Now this was assuming a sphere, and also note the y-axis doesn't start at zero. The non-linearity is due to the changes in the footprint as the depression height first goes above 0. Since real tire geometry start with a much flatter contact area to begin with, it follows that a lot of the initial curve here would not be observed in practice.
Nonetheless, when we're at roughly 1 metric ton of loading, the depression height is about half the radius. Geometrically, I think this point would somewhat resemble the footprint to volume ratio of normal tires, and the above curve's 2nd derivative near that point is thus similar to what we'd see in practice. Furthermore, the adjusted contact area in this example comes out to about 0.06 m^2, which is very similar to what I expect running some simple numbers on the Corolla.
This is much more non-linearity than what I expected, and also a much greater effect from the weight of the car on tire pressure. I would certainly believe that you could cause some problems by failing to account for the impact of loading on tire pressure.
ADDITION:
I really should have assumed a cylinder model. Basically, you imagine all tires are horizontally oriented cylinders, with a hole in the middle for the hub. This is realistic to an extent, and if you have the dimensions, then no correction factor is needed like the above example.
Tire measurements I assumed were:
- R = 0.292 m
- Rin = 0.206 m
- L = 0.711 m
Here, the "L" is the width of the 4 tires, if they were theoretically lined up all next to each other. So this is just multiplying the width of one tire times 4. "Rin" is the radius of the rim. This volume is subtracted out of the total cylinder volume.
These measurements, which are based on outer dimensions, come out to about 95 L. A major difference between this and the above example is thus the volume. However, the fundamental difference in shape is still apparent.
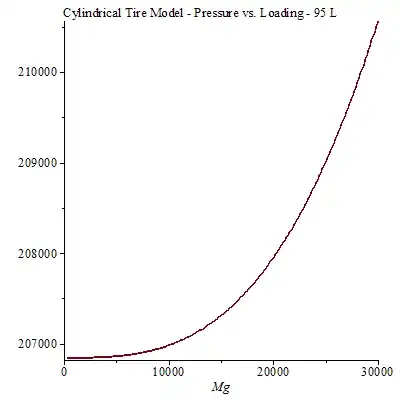
To put this in real terms, if the load is 3 metric tons, tire pressure increases 0.5 psi relative to the unloaded state. It's normal weight causes only about 0.05 psi above the unloaded tire pressure.
The Corolla weighs about 1.3 tons. The maximum legal load is 0.45 tons. Assuming a 0.5 psi error on a pressure gauge seems reasonable.
So my conclusion is that there is no legal way to measure this effect in your garage.




