Why do we fall down when the bicycle slows down?

Question

My question is: It is easy to balance a bicycle when it is moving at a fairly high velocity, say 7 m/s or 25 km/hr. But when a bicycle slows down, it is hard to keep it upright, and the person riding it may thus fall down! Why?

Answer 1

Alright I'll throw my hat into the ring with an answer. The idea that it's an unsolved problem is totally bogus.

When you start to fall to one side or another if you turn the wheel slightly in the direction you're falling the bicycle starts to follow a curved path. There is a force due to friction that deflects the rider's path into a curve:

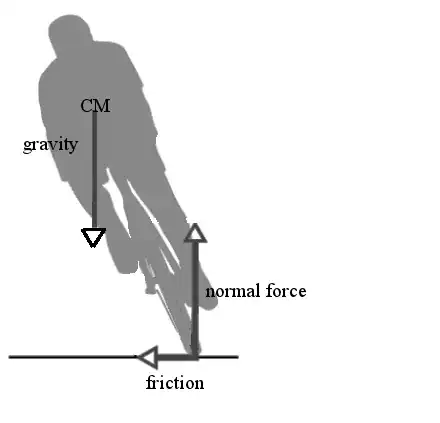
The frictional force pushes against the base of the bike and acts to stand the bike back up vertically. The inward directed friction is what is providing the centripetal acceleration.

This answer becomes obvious when you ask yourself questions like:

• What happens if you are riding quickly when you cross a long patch of ice? The answer is that you slip and fall and no gyroscopic force of the wheels or anything else prevents this.

• What happens if you ride quickly through loose sand? The answer is that if you try to turn (lean) even a little bit too much the sand flows under the bike wheel and doesn't provide enough friction to keep the bike up. You fall over.

• If you want to lean more in a turn do you need to go faster or slower? The answer is faster and it's because you need a greater inward directed force to make up for the lower normal force. The faster an object is going when it is deflected the more force is needed to deflect it which means there is more force available to fight gravity.

While searching for an image for my answer I found this source which explains it the same way: http://electron6.phys.utk.edu/101/CH4/dynamic_stability.htm

So, when you're going slowly on a bicycle the curved path you'd need to follow in order to provide enough friction to stay upright is too tight for the bicycle to turn. Without enough friction to provide the counterbalancing centripetal acceleration the bike will fall. This is also why when you're riding very slowly and trying to stay stable and upright you end up taking very sharp weaving exaggerated turns but when you're traveling quickly you go in almost a straight line. Only the very sharp turns provide enough frictional force to stand the rider back up.

Answer 2

I do not agree with the angular momentum theory: if you were to hop off your bike at speed and let it go by itself, it would not go very far before falling on its side, even less if you put a ~150 lbs sandbag on your saddle. There is indeed an effect caused by momentum, but this is negligible when compared to the actual contribution of the rider.

I agree with KidElephant that when you are going fast, a small adjustment to the steering axis makes a bigger difference in a shorter time. This makes sense when you consider that in order to steer, the bicycle has to lean, and crashing with a bike is analogous to an over-steer condition. When you feel you are getting in an over-steer situation, experienced riders intuitively counter-steer by turning even more into the curve, so that due to the geometry of the bicycle, the bicycle will stabilize itself and become straight again. This, again, is much easier to do at somewhat higher speeds due to the amplification of movements. (a smaller counter-steer movement will have a bigger effect on the bicycle).

I know this source is not exactly a scientific whitepaper, but they seem to have done their research and they cite a few sources. The physics of motorcycles are very similar to that of bicycles. This article supports the claim that gyroscopic forces are not the main actor on motorcycle steering, even though a motorcycle goes at much higher speeds than a bicycle, with much heavier wheels, resulting in a much higher angular momentum.

The gyroscopic precession produced by countersteering supplies the first in a series of "leaning torques" that contribute to lean in the direction of the intended turn.

Though the effect is initially small gyroscopic forces do contribute to leaning though they are secondary to the lean induced by the steering kink.

Answer 3

The answer is that, despite our best efforts, we still can't quite put a finger on it. The gyroscopic forces mentioned by bobie in his answer have been proven not to be sufficient to fully explain why a bike stays upright. It's indeed very surprising that physicists are not able to explain the mechanism behind such an (apparently) simple and ubiquitous device.

This answer on the Bicycle Stack Exchange cites an excellent article on the subject.

Answer 4

So far, it is still an open question as to why bicycles are stable at all. A few ideas have been put forward, but they have been disproved by construction of non-standard bicycles.

The most common explanation is that the wheels on a bike act as a gyroscope, preventing the bike from falling over. A bike was constructed with counter-rotating wheels to test this. The bike had two front wheels, one on the ground and rotating forward, and one off the ground rotating backward. This way, the total angular momentum was zero. However, the bike remained stable.

Another explanation is that the stability of the bike depended on the angle between the frame and the front wheel. Whenever the bike starts tipping to the side, the front wheel turns into the curve to counter-act the tipping. This was also tested by constructing a bike with the front fork going directly up. This also was stable, disproving this hypothesis.

Sources: http://bicycle.tudelft.nl/stablebicycle/StableBicyclev34Revised.pdf

Answer 5

I agree with Brandon's analysis. To add some information on the "why we fall" question:

The bike is unstable in any case in the absence of a driver. To discuss stability with a driver, you must model the driver in some way. It can be modeled by some linear function of the state vector of the bike. There is such a function for any speed > 0 that stabilizes the bike, but that function becomes harder and harder for a human to produce as the bike slows down.

That leads us to the realm of delayed differential equations (DDEs), because of the reaction time of the human driver. The model which Brendon outlined could be modeled as a DDE, with the inclusion of a function that represents the actions of the driver. Then, the regions of stability, with respect to the parameters (the time lag, speed, height etc. of the bike, and any other parameters we introduced in the definition of the controller function) could be determined.

Results obtained by stability analysis of such models can accurately predict, for example at which length a pen is impossible to balance by a human, or how much alcohol someone has to drink so that he is not able to stand up anymore.

Using the results for second order DDEs, I am sure it is possible to derive quantitative results for the bike model as well, eg. at what speed does it become difficult to stay up, ignoring gyroscopic effects.

For those interested in the exact math, I recommend the brilliant monograph of G.Stepan: Retarded Dynamical Systems: Stability and Characteristic Functions.

Answer 6

The question "Why does a slow-moving (or stationary) bicycle fall over?" is kind of a boring one. A stationary bicycle falls over because it is at an unstable equilibrium.

Specifically, a rigid body standing on a surface is at an equilibrium if its center of gravity is above the convex hull of its support (the points where it contacts the surface). If this is not the case, the object is at a disequilibrium, and gravity will cause it to fall over until it reaches a new equilibrium.

An object at equilibrium can be either stable or unstable (or, on the borderline between the two, neutrally stable), depending on whether slightly pushing the object (thereby placing it temporarily at a disequilibrium) will cause it to return to the original equilibrium, or to move to a different one. In particular, a rigid body at equilibrium on a surface is stable (against small perturbations) if and only if:

• its center of gravity is above the interior of the support region, so that slightly moving the center of gravity will not move the object out of equilibrium; or

• more generally, the shape of the contact surface is such that slightly tilting the object will move the contact area in the same direction as the center of gravity, but further. (An example of this case would be e.g. an ellipsoid lying on its side on a flat surface.)

^{(Note that this is not the fundamental definition of stability, which you can find on the Wikipedia page I linked to earlier, or in any decent mechanics textbook. However, it is, IMO, the most convenient stability criterion to apply here, despite its limited applicability to more complex systems.)}

A stationary bicycle, standing upright, is approximately a rigid body standing on two points (where the wheels touch the ground). Thus, its support area is a narrow line connecting those points, and, even if the center of gravity of the bicycle is initially exactly above the line, even the slightest push sideways is enough to move it out of that equilibrium.

(A bicycle, of course, is not a completely rigid body, since it has moving parts. However, for static stability analysis, treating it as if it were rigid turns out to be a good enough approximation.)

Further, while the contact points do move slightly when the bicycle starts to tilt, they move much less than the center of gravity does (since the radius of the wheel tubes is much less than the distance of the center of gravity from the ground). Thus, as soon as the stationary bicycle tilts even slightly to one side, it will be at a disequilibrium, where the effect of gravity is to tilt it further away from the stable equilibrium, until it falls completely over and finds a new equilibrium with a wider support and a lower center of gravity.

In particular, observe that adding a third support point, e.g. in the form of a kick stand, can be enough to create a stable equilibrium at the position where all three points (both wheels and stand) touch the ground, and the center of gravity of the bike lies above the triangle formed by the support points.

---

As for the converse question, "Why doesn't a moving bicycle fall down, then?", that one has already been asked and answered here. In particular, the paper referenced in nibot's answer there provides a pretty definitive explanation.

Summarizing it briefly, there are multiple stabilizing effects (such as the gyroscope effect, the caster effect and the mass distribution of the bicycle — not to mention the active control provided by the person riding it, of course) that can stabilize a moving bicycle, but, as one of the authors of the paper describes at the end of this YouTube video, almost all of them act through a single mechanism: To stay upright, a moving bicycle must turn in the direction it leans towards, and it must turn quickly enough that its support will move sideways faster than its center of gravity.

A slow-moving, or stationary, bicycle will not be able to do this, and therefore is not stable.

One notable exception is that the person riding the bicycle can exert a limited amount of direct control over their center of gravity by shifting their weight and, depending on the caster angle, by turning the handlebars even while stationary. It's not a very strong effect, though, which is why it's very difficult to balance on a stationary bicycle.

(Note that the standard technique for doing this, as described in the Wikipedia article above, essentially cheats a bit by using small amounts of back-and-forth movement. It's still difficult, but not nearly as difficult as it would be if you couldn't do that at all.)