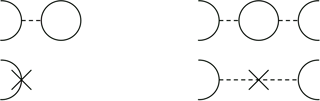$\operatorname{O}(N)$ sigma model at large $N$

Question

I would like to better understand the main principles of large-$N$ expansion in quantum field theory. To this end, I decided to consider a simple toy model with lagrangian (from Wikipedia)

$ \mathcal{L} = \frac{1}{2}(\partial_{\mu} \phi_a)^2-\frac{m^2}{2}\phi_a^2 - \frac{\lambda}{8N}(\phi_a \, \phi_a)^2 $

I aimed to renormalize this theory in all orders of perturbation theory in the leading order of $\frac{1}{N}$. The calculation of counterterms in two loops in the leading order of $\frac{1}{N}$ almost coincides with the corresponding calculation in $\phi^4$ theory. In leading order of $1/N$ the counterterms are (using MS-scheme):

1 Loop:

$\Delta \mathcal{L}_{\phi^4}^{1} = -\lambda^2 \mu^{2\epsilon} \frac{1}{32 \pi^2 \epsilon} \frac{(\phi_a \, \phi_a)^2}{8N}$

$\Delta \mathcal{L}_{\phi^2}^{1} = - \frac{\lambda}{32 \pi^2 \epsilon} \frac{m^2 \phi_a^2}{2}$

2 Loops:

$\Delta \mathcal{L}_{\phi^4}^{1} = -\lambda^3 \mu^{2\epsilon} (\frac{1}{32 \pi^2 \epsilon})^2 \frac{(\phi_a \, \phi_a)^2}{8N}$

$\Delta \mathcal{L}_{\phi^2}^{1} = - (\frac{\lambda}{32 \pi^2 \epsilon})^2 \frac{m^2 \phi_a^2}{2}$

I am quite sure (though I haven't proven it properly yet) that in $n$ loops the leading contribution to counterterms comes from a chain of "fish" diagrams for 4-point Green's function and chain of bubbles for 2-point Green's function (I think, it's quite easy to imagine):

$\Delta \mathcal{L}_{\phi^4}^{1} = -\lambda^{n+1} \mu^{2\epsilon} (\frac{1}{32 \pi^2 \epsilon})^n \frac{(\phi_a \, \phi_a)^2}{8N}+O(\frac{1}{N})$

$\Delta \mathcal{L}_{\phi^2}^{1} = - (\frac{\lambda}{32 \pi^2 \epsilon})^n \frac{m^2 \phi_a^2}{2}+O(\frac{1}{N})$

If this speculation is correct, the summation of the perturbation series is quite trivial (we have geometric series). When we do it and then take limit $\epsilon \rightarrow 0$ we will find that

$\Delta \mathcal{L}^{\infty}_{\phi^2} = \frac{m^2 \phi_a^2}{2}$

$\Delta \mathcal{L}^{\infty}_{\phi^4} = \frac{(\phi_a \phi_a)^2}{8N}$

and hence the total lagrangian is simply (in the leading order of $1/N$).

$\mathcal{L} = \frac{1}{2}(\partial_{\mu} \phi_a)^2$

This result seems to me highly suspicious... Did anybody do a similar calculation? I looked all over the Internet and didn't find anything :( I will be very grateful for remarks and links to books or maybe articles where a similar problem is considered.

Answer 1

A couple of remarks on the comments. As mentioned already, due to the rescaling of $\lambda\to\lambda/N$ in the coupling, you are already in the analogue of the 't Hooft limit, the large $N$ limit is when $\lambda$ is fixed and $N\to\infty$. Intuitively, you need to imagine $\phi^2$ to be extensive so your action is extensive.

You made some mistakes in your calculations. You only need the one loop counter-terms at leading order in $N$: $\Delta\mathcal L_{\phi^2}^1,\Delta\mathcal L_{(\phi^2)^2}^1$. You probably forgot to take into account the effect of the counter-terms in the perturbation series, but you also forgot many diagrams that contribute at the same order of $N$. In order to systematically see which diagrams matter, it is easier to use the following graphical representation:

At leading order, you have the following diagrams for the two and four point connected Green's functions:

At next order of $\lambda$ you have:

I think that you had forgotten the "T" shaped diagram as well as all the counter term diagrams. There is no next order corrections to the counter terms. They were chosen to counter the $\phi$ loops and all new diagrams with more loops is accompanied by the right diagrams with the corresponding counter terms (you will need to work out the symmetry factors to rigorously prove compensation). More generally, counter terms calculated at first order are enough to counter all divergences at any perturbation order of $\lambda$.

You can understand this miraculous compensation and motivate the suggestive graphical choice with the Hubbard-Stratonovitch. The self coupling is now mediated by a new real scalar field $\sigma$: $$ \mathcal L = \frac12\partial\phi^2-\frac{m^2}2\phi^2-\frac i2\sigma\phi^2+\frac N{2\lambda}\sigma^2 $$ This gives the new diagrams:

It is consistent with the previous scheme by viewing the previous $(\phi^2)^2$ vertex as two $\phi^2\sigma$ vertices and a $\sigma$ propagator: $$ -\frac\lambda N = i\frac\lambda Ni $$ To keep track of the $N$ order, the only contribution to the $N$ exponent are by $\sigma$ edges $N$ and $\phi$ loops $1/N$. Viewing the $\phi$ loops as $\sigma$ vertices, in terms of $\sigma$, a diagram has a factor: $$ N^{V-E} $$ for $E$ edges, $V$ vertices. Using the relation: $$ V-E = C-L $$ for $L$ loops, $C$ connected components, the leading order diagram is a completely disconnected one, i.e. the theory is linear and obeys Wick's theorem. For connected diagrams, $C=1$, the leading order is for $L=0$, i.e. tree diagrams. This makes sense as the large $N$ limit is classical. Mathematically, this comes from taking the saddle point after integrating out $\phi$, which is why it is clearer after introducing $\sigma$. Note that it is different from Yang-Mills where you sum over planar diagrams (you do not have double lines, so the whole notion of planarity is ill defined anyways). It also explains why you only need two counterterms at just one loop order: they are the counter terms of the degree 1 and 2 vertex for $\sigma$.

Thus, the bare couplings $m_0^2,\lambda_0$ do diverge as $\epsilon\to0$. It is a rare example where you can explicitly compute the bare couplings as a function of the renormalised ones. You can now compute pretty much anything you want.