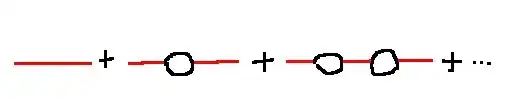$O(N)$ vector model and large $N$

Question

I'm familiar with QFT at the level of QFT by Ryder. I have also consulted many books including QFT by Fradkin which includes $O(N)$ vector model, particularly in $\phi^4$, and nonlinear sigma model, as well as large $N$, even going briefly into planar diagrams and how each Feynman diagram scales in terms of the coupling constant. However, I find the explanation in Fradkin extremely confusing and too brief.

I have also consulted a chapter in a book compiling papers on recent studies in perturbation theory. It came the closest to explaining some stuff just mentioned quickly in Fradkin, however, since the chapter is structured more like a review I still don't understand the detail. An example would be, for $\phi^4$ where $\phi$ has $N$ components, the chapter discussed that the interaction vertex should be drawn as,

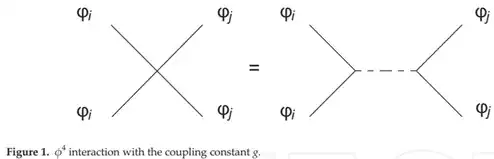
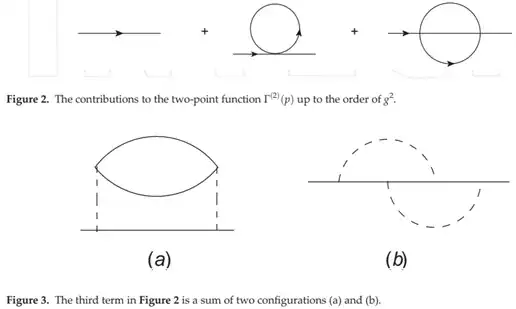
where the left-image is the standard interaction vertex if $N=1$, while the right-image is for arbitrary $N$. In addition, for the two-point function, the contribution upto second-order is given by,

where the third diagram in fig.2 is actually a sum of two diagrams as shown in fig.3. The chapter also talked about the symmetry factors of the third diagram. Specifically, the diagram in fig.3a has a symmetry factor of $4^2 \cdot 2N = 32N$, while the diagram in fig.3b has a symmetry factor of $4^2 \cdot 2^2 = 64$. So the third diagram in fig.2 has a symmetry factor of $32N + 64$ in total.

What does the dashed line mean in Fig.1 and how does it work? Why is the third diagram a sum of two diagrams and how to decompose it? Not knowing even how to interpret the interaction vertex in fig.1 obviously leads me to not know how the symmetry factors work for the third diagram in fig.2. How to count the symmetry factors of those diagrams?

I would also like to ask for any recommendations on this topic that goes into detail such as the loop corrections, detailed explanation on the Feynman diagrams, etc.

Answer 1

Quartic interactions at large $N$ can be simplified by introducing a Hubbard Stratonovich field which interacts with two copies of the original field. That is almost certainly what the chapter you read (and more sources) are doing.

As these papers explain, the action \begin{align} S = \int d^dx \;\frac{1}{2} \partial_\mu \phi_i \partial_\mu \phi_i + \frac{1}{2} \sigma \phi_i \phi_i - \frac{\sigma^2}{4g} \end{align} becomes \begin{align} S = \int d^dx \;\frac{1}{2} \partial_\mu \phi_i \partial_\mu \phi_i + \frac{g}{4} (\phi_i \phi_i)^2 \end{align} once you find the equation of motion for $\sigma$ and plug its solution back in. So these give equivalent formulations of the problem. Since $\sigma$ is like a mass in this case, we can drop $\sigma^2$ for the purposes of studying the critical point because it is an irrelevant operator. E.g. in $d = 3$, it will have dimension 4. We then get the momentum space propagator \begin{align} \left < \sigma(p) \sigma(-p) \right > = 2 \frac{(4\pi)^{d/2} \Gamma(d - 2)}{\Gamma \left ( \frac{d - 2}{2} \right )^2 \Gamma \left ( 2 - \frac{d}{2} \right )} \frac{|p|^{4 - d}}{N} \quad (*) \end{align} for $\sigma$ and the usual one for $\phi_i$ and can use this to do large $N$ perturbation theory. Each dotted line then introduces another factor of $1/N$. Another common convention is to rescale $\sigma$ and $g$ so that the action reads \begin{align} S = \int d^dx \;\frac{1}{2} \partial_\mu \phi_i \partial_\mu \phi_i + \frac{1}{2 \sqrt{N}} \sigma \phi_i \phi_i - \frac{\sigma^2}{4g}. \end{align} After this, the factors of $1/N$ come from the vertices instead and the propagator is $O(1)$.

Now why is (*) correct? It actually isn't if you want to keep track of $\phi$ loops separately. But it is best to use propagators that resum all leading order contributions. So if you let the red line below denote $1/2g$ in accordance with the $\sigma^2$ term in the action, the geometric series

(where each $1/N$ from a pair of vertices is cancelled by a $\phi$ loop) gives \begin{align} \left < \sigma(p) \sigma(-p) \right > = \left [ \frac{1}{2g} + \frac{\Gamma \left ( 2 - \frac{d}{2} \right ) \Gamma \left ( \frac{d - 2}{2} \right )^2}{2(4\pi)^{d/2} \Gamma(d - 2)} |p|^{d - 4} \right ]^{-1} \end{align} and going to low energies makes only the part with $|p|^{4 - d}$ dominate. This is equivalent to noticing that $\sigma$ is a source for $\phi^2$ so it must be such that $\frac{\delta^2 Z}{\delta \sigma(x) \delta \sigma(y)} = \left < \phi^2(x) \phi^2(y) \right >$. In other words, the path integral satisfies \begin{align} Z &= \int D\phi D\sigma e^{-S} \\ &=\int D\sigma \exp \left [ -\int \sigma(p) \left ( \left < \phi^2(p) \phi^2(-p) \right > + \frac{1}{2g} \right ) \sigma(-p) + O(\sigma^3) \frac{dp}{(2\pi)^d} \right ] \end{align} where we can compute the $\phi^2$ two-point function diagrammatically.

Hopefully that gives you a sense of what's going on. Symmetry factors of course have nothing to do with the theory and are found via combinatorics. QFT textbooks should discuss this.