As the Feynman diagram shows above. Does the $s$-channel and $t$-channel stands for exactly same reaction or they have big difference?
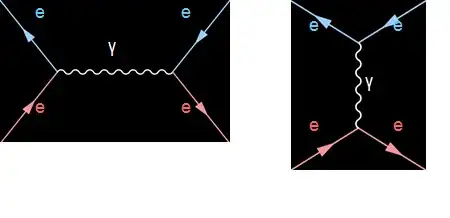
As the Feynman diagram shows above. Does the $s$-channel and $t$-channel stands for exactly same reaction or they have big difference?

To every Feynman diagram we associate a set of integrals which compute the corresponding scattering amplitude according to the Feynman rules. An example of such an amplitude:
$$\mathcal{M}=(-ig)^2\left[ \frac{i}{(p_1-p'_1)^2-m^2}+\frac{i}{(p_1+p_2)^2-m^2}\right]$$
from a tree-level process in scalar Yukawa theory. In the case of two-body to two-body scattering, we denote the incoming momenta as $p_1,p_2$ and the outgoing as $p'_1,p'_2$. We introduce Mandelstam variables which arise commonly in amplitudes:
$$s=(p_1+p_2)^2=(p'_1+p'_2)^2$$ $$t=(p_1-p'_1)^2=(p_2-p'_2)^2$$ $$u=(p_1-p'_2)^2=(p_2-p'_1)^2$$
Our amplitude corresponded to a set of Feynman diagrams:
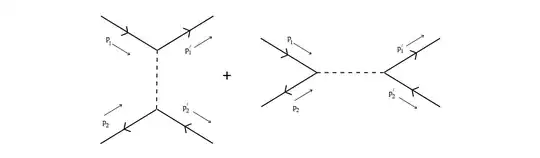
If we substitute for our Mandelstam variables, we see the first diagram has $\mathcal{M}\sim 1/t$ and the second diagram $\mathcal{M}\sim 1/s$. Hence we say the first involves a t-channel and the other an s-channel. The $s$ measures the total centre of mass energy of the collision, whilst $t,u$ are measures of momentum exchanged between the particles.
They represent the same reaction, electron-positron scattering in the two possible ways it can happen to first order.
Feynman diagrams are a pictorial representation of the integrals that have to be added in the perturbative series expansion of the theoretical formula for the scattering cross-section. Like any expansion, there are constants term multiplying each order that determines the contribution of each order which diminishes as the order gets higher. Look at this Taylor series. For perturbative expansions these are the coupling constants, and the terms entering are counted as, first order, second order, etc. In your diagrams, the electromagnetic coupling constant or ~1/137 ensures that the higher terms can be ignored.
The two diagrams are the first order contributions to the cross-section and have to be both taken into account in order to calculate and predict the cross section for the process to first order in the coupling constants involved in the interaction.