What is the difference between $u$ and $t$ channels in Feynman diagrams?

Question

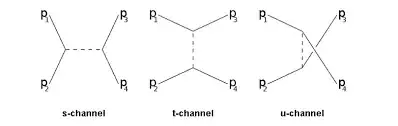
My question is very simple: can someone explain to me the difference between the $u$-channel and the $t$-channel in Feynman diagrams? I can't understand what is the "role change" in $u$-channel.

Answer 1

idk what the problem is, nor why the prior correct answer got a downvote. Nevertheless, I'll try. I included the diagram from the link in the OP.

That answer used Moeller scattering as an example, which is the classic QED example. It may help to look at it as it approaches a 1D problem, that is, as $\theta \rightarrow 0$.

So we're scattering an electron beam off atomic electrons in a foil target (e.g. SLAC: E-158 https://www.slac.stanford.edu/exp/e158/).

In the t-channel, as $\theta_{lab} \rightarrow 0$, you have $t\rightarrow 0$ and it's forward scattering, transferring very little momentum to the atomic target (ofc, you detected the scattered electron beam in a narrow acceptance spectrometer, a la SLAC's end-station A's famous 8 GeV and defunct 20 GeV shown here (2 mile accelerator is to viewer's left):

)

This is indistinguishable from the u-channel, where your beam electron clobbers the target electron and kicks it out nearly straight ahead, with the beam energy. Here $u\rightarrow 0$.

This is not a background processes where backscattering t-channel events are mistaken identified as forward u-channel events, rather: they are quantum mechanically indistinguishable and hence they interfere at the amplitude level.

It's no different from Young's double slit experiment. "Did the electron go through the left slit or the right slit?" is treated the same way as "Was this a forward event t-channel event a forward u-channel event?"

Ofc: it was both, and hence you need to include interference.

(Now the experiment I referenced looks at interference in the exchanged boson: was it a $ \gamma$ or a $Z^0$? You can't know, and the interference term leads to a small but measurable parity violating term. Meanwhile, the $Z^0$ only term is the weak interaction (squared) and is too small to observe in the presence of electromagnetic scattering).

Answer 2

Essentially, you need these two channels to account for a possible particle exchange.

Say, for example, that you have a scattering of two electrons in, and two out. Let us call the incoming electrons $A$ and $B$, and the outgoing electrons $C$ and $D$. At tree level, you have two diagrams:

1. $A$ emits/absorbs a photon and comes out as $C$, while $B$ absorbs/emits the photon and comes out as $D$, and
2. $A$ emits/absorbs a photon and comes out as $D$, while $B$ absorbs/emits the photon and comes out as $C$.

You need to account for both processes because the electrons are indistinguishable. It is not possible for you to tell which electron, $A$ or $B$, came out as $C$. Hence, you need to account for both possibilities. One of these possibilities is the $t$-channel, the other one is the $u$-channel.

But then which option is $t$ and which option is $u$? That is a matter of convention. You need to call one of them $t$, and the other $u$, but which one is which is up to you and how you choose to define your Mandelstam variables. Usually, people like to define the $t$ variable in a way that the $t$-channel is the one in which the "most similar particles" are connected if possible in that particular process, but this is just a choice.

Note: my labeling of electrons as $A$, $B$, etc is a bit inconsistent with the point I'm making (electrons are indistinguishable), but you could use their momenta as a "label" at the vertex they enter in the diagram.

Answer 3

I don't think they're qualitatively different, rather, they're just the two possibilities that appear when two particles exchange momentum. This has a greater importance when the final state consists of two different particles. If the two final particles are identical, then the $t$ and $u$ channels are functionally the same, their only difference representing labeling. But now consider an inteaction term $\mathcal{L}_I$ that depends on two kinds of fields (scalar for simplicity), $\phi$ and $\psi$, perhaps $\mathcal{L}_I \propto \phi^2\psi^2$ (so that it's equivalent to a $\phi^4$ theory). Let's say particles 1 and 3 are $\phi$ and 2 and 4 are $\psi$. Then there is an obvious difference between the two channels. The $t$ channel is a scattering event where the entering particles aren't exchanged, while the $u$ channel "exchanges" the particles.