What is the feedback \$\beta\$ for this resistor feedback?

Question

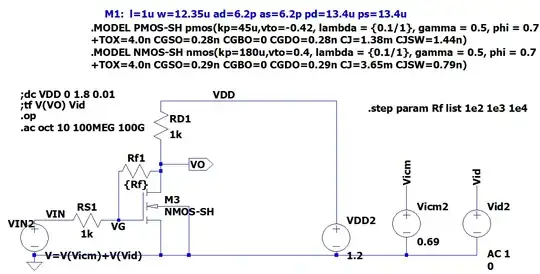
The first is the schematics from NMOS4 with parasitic capacitance:

What is the feedback \$\beta\$ for this resistor feedback? And Should we include the capacitor \$C_{gd}\$ for this feedback?

The following is the asc file for whom is interested:

Version 4
SHEET 1 880 808
WIRE -224 16 -368 16
WIRE 32 16 -224 16
WIRE -368 32 -368 16
WIRE -368 160 -368 112
WIRE -304 160 -368 160
WIRE -368 176 -368 160
WIRE -368 176 -384 176
WIRE -368 208 -368 176
WIRE -304 256 -368 256
WIRE 192 256 192 208
WIRE 352 256 352 208
WIRE -608 288 -656 288
WIRE -576 288 -608 288
WIRE -464 288 -464 176
WIRE -464 288 -496 288
WIRE -416 288 -464 288
WIRE 32 288 32 16
WIRE -368 368 -368 304
WIRE -368 368 -656 368
WIRE -304 368 -304 256
WIRE -304 368 -368 368
WIRE 32 368 -304 368
WIRE 192 368 192 336
WIRE 192 368 32 368
WIRE 352 368 352 336
WIRE 352 368 192 368
WIRE -656 384 -656 368
FLAG -656 384 0
FLAG -224 16 VDD
FLAG -464 288 VG
FLAG -304 160 VO
IOPIN -304 160 Out
FLAG 192 208 Vicm
FLAG 352 208 Vid
FLAG -608 288 VIN
SYMBOL nmos4 -416 208 R0
WINDOW 3 56 60 Left 2
SYMATTR Value NMOS-SH
SYMATTR InstName M1
SYMATTR Value2 l=1u w=12.35u ad=6.2p as=6.2p pd=13.4u ps=13.4u
SYMBOL voltage 32 272 R0
WINDOW 123 0 0 Left 0
WINDOW 39 0 0 Left 0
SYMATTR InstName VDD2
SYMATTR Value 1.2
SYMBOL voltage 192 240 R0
WINDOW 123 0 0 Left 0
WINDOW 39 0 0 Left 0
SYMATTR InstName Vicm2
SYMATTR Value 0.69
SYMBOL voltage 352 240 R0
WINDOW 3 24 152 Left 2
WINDOW 123 24 124 Left 2
WINDOW 39 0 0 Left 0
SYMATTR Value 0
SYMATTR Value2 AC 1
SYMATTR InstName Vid2
SYMBOL bv -656 272 R0
WINDOW 0 -60 23 Left 2
SYMATTR InstName VIN2
SYMATTR Value V=V(Vicm)+V(Vid)
SYMBOL res -368 160 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName Rf1
SYMATTR Value {Rf}
SYMBOL res -384 16 R0
SYMATTR InstName RD1
SYMATTR Value 1k
SYMBOL res -480 272 R90
WINDOW 0 0 56 VBottom 2
WINDOW 3 32 56 VTop 2
SYMATTR InstName RS1
SYMATTR Value 1k
TEXT -528 -152 Left 2 !.MODEL PMOS-SH pmos(kp=45u,vto=-0.42, lambda = {0.1/1}, gamma = 0.5, phi = 0.7\n+TOX=4.0n CGSO=0.28n CGBO=0 CGDO=0.28n CJ=1.38m CJSW=1.44n)
TEXT -528 -96 Left 2 !.MODEL NMOS-SH nmos(kp=180u,vto=0.4, lambda = {0.1/1}, gamma = 0.5, phi = 0.7\n+TOX=4.0n CGSO=0.29n CGBO=0 CGDO=0.29n CJ=3.65m CJSW=0.79n)
TEXT -496 -184 Left 2 ;M1:  l=1u w=12.35u ad=6.2p as=6.2p pd=13.4u ps=13.4u
TEXT -688 48 Left 2 !.op\n.ac oct 10 100MEG 100G
TEXT -688 24 Left 2 !;tf V(VO) Vid
TEXT 104 32 Left 2 !.step param Rf list 1e2 1e3 1e4
TEXT -688 0 Left 2 !;dc VDD 0 1.8 0.01

You can easily see that $V_G = \frac{R_{f1}}{R_{S1} + R_{f1}} V_{in} + \frac{R_{S1}}{R_{S1} + R_{f1}} V_{out}$, so the feedback factor should be clear. — internet, Feb 11 '24 at 10:21
@internet I have no idea how you derive this formula. Please explain a little more — kile, Feb 11 '24 at 14:52
I've rolled this question back to how it was when I made my answer. The addition of the circuit (that was rolled-back) is starting to take the question down a route of asking how to break the loop in order to determine the feedback factor and, that subject is being covered in incidental comments below my answer i.e. it is not the primary question that I answered. — Andy aka, Feb 11 '24 at 15:04
@internet I finally understand you formula. But I still couldn't figure out the feedback factor. Could you help me out? — kile, Feb 11 '24 at 20:43

score 3 · Accepted Answer · answered Feb 11 '24 at 09:46

3

What is the feedback β for this resistor feedback?

This boils down to how much the output signal is attenuated at the gate (with the input VIN set to zero. So, it's a simple potential divider involving Rf1 and RS1.

You should also take into account the AC small signal loading effect of Rf1 and RS1 on the drain voltage. This is usually not negligible. They are, in effect, a series connection in parallel with Rd1.

Should we include the capacitor Cgd for this feedback?

That's completely up to you. If you want accuracy then yes.

answered Feb 11 '24 at 09:46

Andy aka

456,226
28
367
807

Where do we break the loop and add test voltage circuit? Could you show me if you have time? – kile Feb 11 '24 at 11:34
@kile I don't understand your comment. What are you trying to achieve? – Andy aka Feb 11 '24 at 12:12
This feedback is negative in my opinion. in order to find the feedback $\beta$ we need break up the circuit – kile Feb 11 '24 at 13:11
@LvW What are the differences V(VG) and V(G)? I think they the same thing. ratio V(VG)/V(G) is 1 – kile Feb 11 '24 at 14:44
@kile You don't need to do that. Inject a current into the drain and monitor the voltage on the gate. I've rolled back your question for good reasons by the way. – Andy aka Feb 11 '24 at 15:07
1

@kile - No, you are not correct. Simple math: The DIFFRENCE V(G)-V(VG) is identical to the value of the source but the ratio can assume any values. Two examples: 1.5/0.5=3 and 11/10=1.1. Injecting such a test voltage into the opening is the classical method for finding the loopgain. – LvW Feb 11 '24 at 16:24
@kile - I forgot to mention that - of course - the input Vin2 must be set to zero for loopgain analysis. – LvW Feb 11 '24 at 16:31
@kile I'm sorry you are getting hit from two fronts now. If LvW wants to make a formal answer and explain why his method is preferred that' fine by me but, remember, this question is answered now so, maybe it's better to move on and ask this as a new question. – Andy aka Feb 11 '24 at 17:42
@kile If we are done here, please take note of this: What should I do when someone answers my question. If you are still confused about something then leave a comment to request further clarification. – Andy aka Feb 13 '24 at 21:51
You have provide the $\beta$ value yet – kile Feb 13 '24 at 22:09
@kile do you understand how to use a potential divider formula: beta equals RS1/(RS1 + RF1) – Andy aka Feb 13 '24 at 22:12
@Andyaka Now I will approve your answer. You haven't specified what the numerator is before. It could also be RF1/(RS1 + RF1) – kile Feb 13 '24 at 22:18
Don't forget that if you need to take into account Cgd, it goes in parallel with RF1 @kile – Andy aka Feb 13 '24 at 23:25

What is the feedback \$\beta\$ for this resistor feedback?

1 Answers1

Linked