How to calculate the feedback loop gain with feedback \$\beta\$

Question

The following is from the book Design of Analog CMOS Integrated Circuit, page 319.

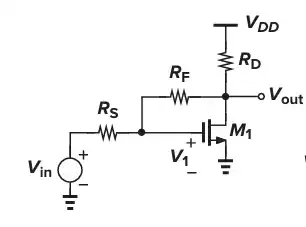
Let's break the loop at the gate of M1.

$$V_{out} = - V_T g_m \biggr[ (R_S + R_F) \parallel R_D\biggr] $$

$$V_F = V_{out} \frac{R_S} {R_F + R_S} $$

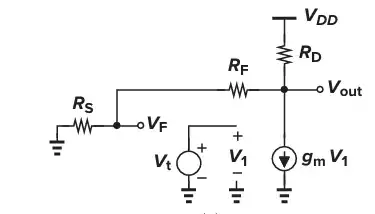
$$\Rightarrow \frac{V_F} {V_T} = - \frac{g_m R_S R_D} {R_D + R_S + R_F}$$

$$\Rightarrow L(s) = \frac{V_F} {V_T} = -\frac{g_m R_S R_D} {R_D + R_S + R_F}$$

\$\beta\$ negative since it's negative feedback.

$$V_G = \frac{V_{in} R_F + V_{out} R_S} {R_F + R_S} $$

$$\Rightarrow \beta = -\frac{R_S} {R_S + R_F}$$

$$A_{v, close} = \frac{L} {1 + L} \frac{1} {\beta} = \frac{g_m R_D (R_F + R_S)} {R_D + R_S + R_F - g_m R_D R_S} $$

However, the exact close loop gain is

$$A_{v,close} = \frac{(1 - g_m R_F) R_D} {R_D + R_F + R_S + R_D R_S g_m}$$

You can see how I derive this exact close loop gain from my previous post previous post.

the closed-loop frequency response of a feedback circuit can be expressed without reference to A(s)

$$A_{CL} = \frac{1} {\beta} \frac{L(s)} {1 + L(s)} $$

In conclusion, these two gains are not the same. Is there anything wrong here?

Answer 1

When you write the formula in this format, you can easily see that \$ \frac{1}{\beta} \$ should be the ideal closed-loop gain when the loop gain approaches infinity.

$$\frac{1}{\beta} = \lim_{{L \to \infty}} \frac{1}{\beta} \cdot \frac{L(s)}{1 + L(s)}$$

When the loop gain approaches infinity, you can see that \$V_{GS}\$ should be 0, and from that, you can easily derive \$V_{out}/V_{in}\$ and \$\beta\$: $$ \frac{V_{\text{out}}}{V_{\text{in}}} = -\frac{R_{\text{F}}}{R_{\text{S}}} \quad \text{and} \quad \beta = -\frac{R_{\text{S}}}{R_{\text{F}}} $$

You may want to check Middlebrook's feedback theory lectures if you want to learn more about this.

Answer 2

@kile: I think, the loop gain calculation L(s) is correct.

However, can you please explain how you arrived at the term Av,close=[L/(1+L)]/beta ?

I rather think, that we always must use the form:

Av,close=af*Ao/(1+L) with loop gain L=Ao * beta and the forward damping factor af.

Added (edit): This forward damping factor (af) gives the input signal at the amplifiers input (gate) when there is no signal coming back from the amplifier output: af=(Rf+Rd)/(Rs+Rf+Rd)