Linear algebra (Osnabrück 2024-2025)/Part II/Lecture 50
See Also
 A tetrahedron (a pyramid with equilateral triangles as faces).
A tetrahedron (a pyramid with equilateral triangles as faces). An octahedron.
An octahedron. A dodecahedron, it has twelve faces.
A dodecahedron, it has twelve faces. An icosahedron, with 20 faces ...
An icosahedron, with 20 faces ...
Every symmetry of a solid in space (for example, a cube) is in particular a distance-preserving, affine-linear mapping of the space. The set of all distance-preserving linear (proper) mappings of the space forms the so-called orthogonal group (or , if we insist that the determinant is ). This is a big infinite group. However, it is interesting that its finite subgroups can be described explicitly. These finite subgroups can be realized as the symmetry group of a suitable geometric object. The fact that a simple classification of these finite symmetry groups is possible rests on intrinsic structural properties of the space itself, and yields among other things a precise version of the fact that there exists only five regular polyhedra (the platonic solids). We have dealt with the cube in Example 49.2 , it allows proper symmetries. Another important example is the tetrahedron.
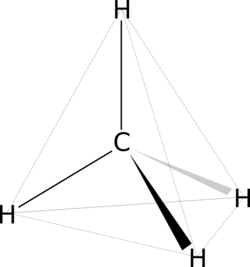
We consider a tetrahedron, that is, a pyramid with four equilateral triangles as faces. The simplest model for this arises when we take every second vertex of a cube; for example, the vertices
The distance of the vertices to the origin is , and the edges have length . A proper symmetries of the tetrahedron is also a proper symmetry of the corresponding cube.[1]
The symmetries of the tetrahedron can be described in several ways. Under such a symmetry, the vertices are mapped to each other. Also, the lines corresponding to the vertices (keeping in mind the relation with the cube, these are the space diagonals of the cube) are mapped to each other. Therefore, the vertices of the cube are also mapped to each other. Hence, the symmetry group of the tetrahedron is a subgroup of the symmetry group of the cube. There are rotations around the axes given by a vertex and the opposite faces, and rotations around the axes between the midpoints of the edges, see also Exercise 49.16 .
The alternating group contains (for ) elements. According to Exercise 50.25 , the tetrahedral group is isomorphic zu .
In the following, we want to understand all finite subgroups of the proper symmetry group of the space. For an affine space over a Euclidean vector space, this group consists of all affine-linear proper isometries, including the translations. However, for a finite subgroup, the translations are irrelevant. The following lemma says that every finite subgroup of the affine symmetry group is also a subgroup of the linear symmetry group.
Let be a finite subgroup of the isometry group of an affine space over a Euclidean vector space . Then the isometries of the group have a common
fixed point. In particular, such a group can be realized as a subgroup of .Let the order of the group. Let be an arbitrary point. We consider the barycentric combination[2]
Because every is an affine-linear mapping, due to Lemma 30.10 we have the equality
As we have a group, the set , , runs through all elements of the group. Hence, the expression on the right equals ; therefore, is a fixed point for all . We choose now as the origin, and we can identify with . According to Lemma 30.12 , the affine-linear mappings become linear mappings. Thus, we obtain as a subgroup of the isometry group of . Since is isometric to , endowed with the standard inner product, we obtain .
- Finite symmetry groups in the plane
We first consider the symmetry groups of the plane.
Let be a finite subgroup of the linear proper isometry group of the real plane. Then is a
cyclic group.Every element in is, due to Theorem 34.4 , a rotation of the plane with a determined angle . We consider the surjective group homomorphism
which assigns to an angle its corresponding rotation. Let be the preimage of under this mapping; that is, consists in all rotation angles of those rotations that belong to . The group is generated by a representing system for the elements of and by . In particular, is a finitely generated subgroup of . Since every group element of has a finite order, every has the form with a rational number . This means that id a finitely generated subgroup of . Hence, is isomorphic to a finitely generated subgroup of the rational numbers. According to Exercise 44.5 , is cyclic, say , with a uniquely determined angle . Then the group , which is the image group of , is cyclic as well.
The uniquely determined angle is
,
where is the group order of . The group consists in the rotation matrices
If we allow also improper symmetries, then there is another family of finite subgroups of the , the dihedral groups.
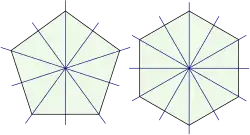
For a regular -gon (), the group of all (proper or improper) linear symmetries
is called the dihedral group .The dihedral group consists of the rotations of a regular -gon and of the reflections at the following axis through the origin:
if is odd, the axes are given by a vertex and midpoint of the opposite edge.
In both cases, the dihedral group consists of elements.
- Systems of semiaxes
We consider now the three-dimensional situation.
Let be a finite subgroup of the group of proper linear isometries. Every element , , is, according to Theorem 34.8 , a rotation around a uniquely determined axis . In particular, for a finite group of symmetries, only finitely many rotation axis are involved. Every group element acts as a permutation on the set of the rotation axes, and this condition narrows down the possible groups. A rotation axis has two rays, and it will turn out to be useful to look at the action of the group on this set of rotation rays, or semiaxes.
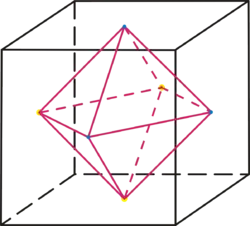
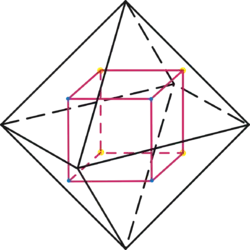
For a cube, there are three different types of rotation axes: there are three rotation axes given by the centers of the faces, there are four rotation axes given by the vertices, and there are six rotation axes given by the midpoints of the edges. If we consider the intersection points of these axes with the sphere of radius , then we obtain
points. These points correspond to the semiaxes. Here, for any two of the vertices, there exists at least one
symmetry of the cube that transforms these points into each other, and also for any two midpoints of the edge, and for any two of the face centers. Every symmetry permutes these characteristic points. If we fix an axis
(or an intersecting point),
then we may consider the set of all symmetries that has this line as its axis. It is also possible to map an axis to itself without being the rotation axis. In this case, the opposite points are mapped to each other.
Let be a finite subgroup of the group of proper linear isometries in . Every line through the origin that appears a s rotation axis of some element , is called an axis of . Any ray of such a rotation axis is called a semiaxis of the group. The set of all these semiaxes is called the system of semiaxes of , and it is denote by . Two semiaxes are called equivalent if there exists a with . The equivalence classes
of this equivalence relation are called classes of semiaxes.Because every rotation different from has a unique rotation axis, the system of semiaxes of a finite symmetry group is finite (in fact, its number is at most ). If is a semiaxis, and , then also is a semiaxis: If the rotation axis of is the axes defined by , then
This also shows that "equivalent semiaxes“ defines indeed an equivalence relation.
Example
For a cube, the semiaxes are represented by the vertices, the centers of the faces, and the midpoint of the edges. These three types are the equivalence classes, that is, the semiaxes classes. The comparison with the octahedron shows that the concepts of a semiaxis for a symmetry group is more appropriate than talking about vertices, edges, midpoints.
Example
For a tetrahedron, there are four axes given by a vertex and the center of the opposite face, and four axes given by midpoints of edges. here, the semiaxes belonging to opposite edges, are all equivalent to each other. However, the semiaxes belonging to a vertex and a face are not equivalent, the semiaxis of the vertex side is not equivalent to the semiaxes of the face side.
This example also shows that the semiaxes belonging to a rotation axis are not necessarily equivalent to each other.
- The stabilizer
Let be a finite subgroup of the group of proper linear isometries in . For a semiaxis of , set
equivalent semiaxes and , the groups and
are isomorphic. In particular, they have the same order.Let , which exists, because the two semiaxes are equivalent to each other due to the condition. Then we get immediately the group isomorphism
Because of
this inner automorphism of maps indeed the subgroups to each other.
Note that is a subgroup of . It is called the stabilizer group of the semiaxis . The lemma tells us that equivalent semiaxes hace isomorphic stabilizer groups. If , and is a semiaxis in the class of semiaxes , and if the subgroup contains elements, then there exist in exactly semiaxes. The fixed semiaxis defines a surjective mapping
Here, is sent to , and for every semiaxis there exist preimages.
- Footnotes
- ↑ When we start with a cube, we get a tetrahedron by taking every second vertex of the cube.
- ↑ This is also the center of gravity of the points involved.
| << | Linear algebra (Osnabrück 2024-2025)/Part II | >> PDF-version of this lecture Exercise sheet for this lecture (PDF) |
|---|