Linear algebra (Osnabrück 2024-2025)/Part II/Lecture 49

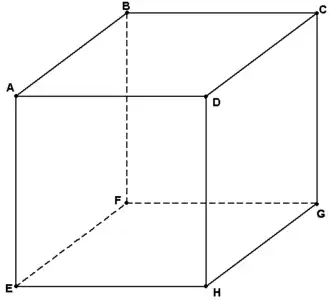
We consider a cube ${\displaystyle {}W\subset \mathbb {R} ^{3}}$, with sides of length ${\displaystyle {}2}$, and the origin as its center. Thus, the vertices are

${\displaystyle (\pm 1,\pm 1,\pm 1).}$

We ask what are the possibilities to transform the cube into itself. By this, we mean that the cube shall not be deformed in any way, the cube is considered rigid, and the motion should be realizable in the physical world. We talk about a (proper) motion of the cube. During such a motion, the center of the cube does not change its position, and faces are mapped to faces, edges to edges, vertices to vertices. Also, the centers of the faces are mapped to centers of faces, and opposite centers of faces are mapped to opposite centers of faces. The centers of faces are the six points

${\displaystyle (\pm 1,0,0),\,(0,\pm 1,0),\,(0,0,\pm 1).}$

If the point ${\displaystyle {}(1,0,0)}$ is mapped to the face center ${\displaystyle {}S}$, then ${\displaystyle {}(-1,0,0)}$ is mapped to the opposite point, that is, ${\displaystyle {}-S}$. Every face center ${\displaystyle {}S}$ is allowed, but this does not determine the motion. For the face center ${\displaystyle {}(0,1,0)}$, there are four possible image points (only ${\displaystyle {}S}$ and ${\displaystyle {}-S}$ are excluded), because the cube can be rotated around the axis given by ${\displaystyle {}S}$ by a multiple of ${\displaystyle {}90}$ degree. These rotations correspond to the possibilities to move the point ${\displaystyle {}(0,1,0)}$ to one of the four remaining face centers. The choice of the second face center ${\displaystyle {}T}$ determines the motion uniquely. How clear is that?

To understand this, the following observations are useful.

1. Motions can be performed after another, that is, if we have two motions of the cube ${\displaystyle {}}$ \varphi ${\displaystyle {}}$, then the composition ${\displaystyle {}\psi \circ \varphi }$ is defined, which performs first ${\displaystyle {}\varphi }$ and then ${\displaystyle {}\psi }$.
2. The identical motion, which moves nothing, is a motion. If man zu of a arbitraryen Bewegung the identische Bewegung davor or danach durchführt, so ändert the the Bewegung not.
3. For a motion ${\displaystyle {}\varphi }$, there exists the opposite motion (or "inverse motion“) ${\displaystyle {}\varphi ^{-1}}$, which has the property that the compositions ${\displaystyle {}\varphi ^{-1}\circ \varphi }$ and ${\displaystyle {}\varphi \circ \varphi ^{-1}}$ are just the identity.

With these observation, we can understand the principle mentioned above: assume that there are two motions ${\displaystyle {}\varphi }$ and ${\displaystyle {}\psi }$, both sending ${\displaystyle {}(1,0,0)}$ to ${\displaystyle {}S}$ and ${\displaystyle {}(0,1,0)}$ to ${\displaystyle {}T}$. Let ${\displaystyle {}\psi ^{-1}}$ denote the inverse motion of ${\displaystyle {}\psi }$. Then we consider the composed motion

${\displaystyle {}\theta =\psi ^{-1}\circ \varphi \,.}$

This motion hat the property that ${\displaystyle {}(1,0,0)}$ is mapped to ${\displaystyle {}(1,0,0)}$ and that ${\displaystyle {}(0,1,0)}$ is mapped to ${\displaystyle {}(0,1,0)}$, as ${\displaystyle {}\varphi }$ sends ${\displaystyle {}(1,0,0)}$ to ${\displaystyle {}S}$, and ${\displaystyle {}\psi ^{-1}}$ sends ${\displaystyle {}S}$ back to ${\displaystyle {}(1,0,0)}$ (and accordingly for ${\displaystyle (0,1,0)}$). This means that ${\displaystyle {}\theta }$ has the property that ${\displaystyle {}(1,0,0)}$ as well as ${\displaystyle {}(0,1,0)}$ are sent to themselves, that is, these points are fixed points of the motion. But this implies that the ${\displaystyle {}x,y}$-plane is fixed. The only physical motion of the cube that fixes this plane is the identical motion. Therefore, ${\displaystyle {}\psi ^{-1}\circ \varphi =\operatorname {Id} }$, and ${\displaystyle {}\varphi =\psi }$. Note that the reflection an the ${\displaystyle {}x,y}$-plane swaps the points ${\displaystyle {}(0,0,1)}$ and ${\displaystyle {}(0,0,-1)}$, but this is a so-called improper motion; it can not be performed in the physical world.

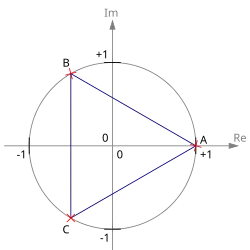
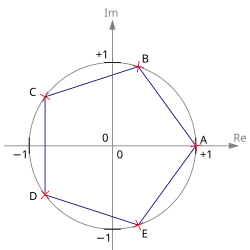
We consider the unit circle

${\displaystyle {}S^{1}={\left\{(x,y)\in \mathbb {R} ^{2}\mid x^{2}+y^{2}=1\right\}}\,.}$

The circle can be parametrized by the trigonometric functions. These assign, for an angle ${\displaystyle {}\alpha \in [0,2\pi )}$ (with respect to the ${\displaystyle {}x}$-axis, counter-clockwise), the corresponding point

${\displaystyle (\cos \alpha ,\sin \alpha )}$

on the circle. A uniform subdivision of the interval ${\displaystyle {}[0,2\pi ]}$ in ${\displaystyle {}n}$ pieces of the same length, given by the boundaries

${\displaystyle 0,\,{\frac {2\pi }{n}},\,2{\frac {2\pi }{n}},\,3{\frac {2\pi }{n}},\ldots ,(n-1){\frac {2\pi }{n}},\,n{\frac {2\pi }{n}}=2\pi ,}$

yields a uniform subdivision of the circle with the points

${\displaystyle (1,0),\,\left(\cos {\frac {2\pi }{n}},\,\sin {\frac {2\pi }{n}}\right),\,\left(\cos 2{\frac {2\pi }{n}},\,\sin 2{\frac {2\pi }{n}}\right),\,\left(\cos 3{\frac {2\pi }{n}},\,\sin 3{\frac {2\pi }{n}}\right),\ldots ,\left(\cos(n-1){\frac {2\pi }{n}},\,\sin(n-1){\frac {2\pi }{n}}\right).}$

These points are the vertices of a regular ${\displaystyle {}n}$-gon. The regelular "2-gon“ has the vertices ${\displaystyle {}}$ (1,0) ${\displaystyle {}}$, the regular (equilateral) trianlge has the vertices

${\displaystyle \left(1,\,0\right),\,\left(-{\frac {1}{2}},\,{\frac {\sqrt {3}}{2}}\right),\,\left(-{\frac {1}{2}},\,-{\frac {\sqrt {3}}{2}}\right),}$

the regular ${\displaystyle {}4}$-gon (square) has the vertices

${\displaystyle (1,0),\,(0,1),\,(-1,0),\,(0,-1),}$

We consider a regular ${\displaystyle {}n}$-gon as a rigid object, and we are interested how it can be transformed to itself. The origin is the center (of gravity) of the ${\displaystyle {}n}$-gon, a motion of the ${\displaystyle {}n}$-gon maps this center to itself. Because such a motion does not change the length, the point ${\displaystyle {}(1,0)}$ is sent to a vertex; only these points have distance one from the origin. A motion does not change angles; therefore, the adjacent vertex ${\displaystyle {}\left(\sin {\frac {2\pi }{n}},\,\cos {\frac {2\pi }{n}}\right)}$ is sent to an adjacent vertex of the image point of ${\displaystyle {}(1,0)}$. For a proper motion (realizable in the plane in the physical sense!), also the ordering (the "orientation“) of the vertices is preserved, so that the only proper motions of a regular ${\displaystyle {}n}$-gon are the rotations by a multiple of ${\displaystyle {}2\pi /n}$.

If we also allow improper symmetries, then there are also the reflections at an axis; for ${\displaystyle {}n}$ even, the reflection axes run through two opposite vertices, or two opposite edge centers, and bei ${\displaystyle {}n}$ odd, the reflection axes run through a vertex and an opposite edge center.

Let ${\displaystyle {}n}$ be fixed, and set ${\displaystyle {}\alpha =2\pi /n}$, and let ${\displaystyle {}\varphi }$ denote the rotation of the ${\displaystyle {}n}$-gon around ${\displaystyle {}\alpha }$ counter-clockwise. Then every rotation of the ${\displaystyle {}n}$-gon can be written as ${\displaystyle {}\varphi ^{k}}$, with a uniquely determined ${\displaystyle {}k}$ between ${\displaystyle {}0}$ and ${\displaystyle {}n-1}$. Here, ${\displaystyle {}\varphi ^{0}=\operatorname {Id} }$ is the rotation by zero degree (the identical motion). If ${\displaystyle {}\varphi }$ is performed ${\displaystyle {}n}$-times, then we have done one complete rotation. Looking at the result, this is just the identical motion. More generally, when ${\displaystyle {}\varphi }$ is performed ${\displaystyle {}m}$-times, then the result (that is, the effective motion) does only depend on the remainder ${\displaystyle {}m\mod n}$. The inverse motion of ${\displaystyle {}\varphi ^{k}}$ is ${\displaystyle {}\varphi ^{-k}}$, that is, ${\displaystyle {}k}$-times the motion backwards, but this is the same as ${\displaystyle {}\varphi ^{(n-k)}}$. All rotations of a regular ${\displaystyle {}n}$-gon form a cyclic group of order ${\displaystyle {}n}$.