Linear algebra (Osnabrück 2024-2025)/Part II/Lecture 48

Residue class rings

On the residue class group for a normal subgroup in a group, there are quite often additional structures available, if the group and the normal subgroup fulfill certain properties. In the last lecture, we have looked at residue class spaces for a linear subspace. Here, we discuss briefly residue class rings for an ideal in a commutative ring. We recall the definition of a ring homomorphism.

Lemma

Let ${\displaystyle {}R}$ and ${\displaystyle {}S}$ be commutative rings, and let

${\displaystyle \varphi \colon R\longrightarrow S}$

be a ring homomorphism. Then the kernel

${\displaystyle {}\operatorname {kern} \varphi ={\left\{f\in R\mid \varphi (f)=0\right\}}\,}$

is an ideal

in ${\displaystyle {}R}$.

Proof

See Exercise 48.1 .

${\displaystyle \Box }$

Due to Lemma 48.2 , the kernel of a ring homomorphism is an ideal. We will construct, for any given ideal ${\displaystyle {}I\subseteq R}$ in a (commutative) ring, a commutative ring ${\displaystyle {}R/I}$ and a surjective ring homomorphism

${\displaystyle R\longrightarrow R/I,}$

dessen kernel is the ideal ${\displaystyle {}I}$. Therefore, ideals and kernels of ring homomorphisms are essentially equivalent objects, in the same way as, in group theory, normal subgroups and kernels of group homomorphisms are the same. In fact, the same homomorphism theorems hold again, and follow easily from the group situation.

Definition

Let ${\displaystyle {}R}$ be a commutative ring, and let ${\displaystyle {}I\subseteq R}$ be an ideal in ${\displaystyle {}R}$. For ${\displaystyle {}a\in R}$, the subset

${\displaystyle {}a+I={\left\{a+f\mid f\in I\right\}}\,}$

is called the coset of ${\displaystyle {}a}$ to the ideal ${\displaystyle {}I}$. Every subset of this form is called a coset to ${\displaystyle {}I}$.

These cosets are just the cosets of the (additive) subgroup ${\displaystyle {}I\subseteq R}$, which is a normal subgroup, as ${\displaystyle {}(R,+,0)}$ is a commutative group. Two elements ${\displaystyle {}a,b\in R}$ define the same coset, that is, ${\displaystyle {}a+I=b+I}$, if and only if their difference ${\displaystyle {}a-b}$ belongs to the ideal. We also say that ${\displaystyle {}a}$ and ${\displaystyle {}b}$ represent the same coset.

We have to show that these mappings (that is, addition and multiplication) are well-defined, that is, independent of the choice of representatives, and that the ring axioms are fulfilled. As ${\displaystyle {}I}$ is, in particular, a subgroup of the commutative group ${\displaystyle {}(R,+,0)}$, it is a normal subgroup, so that ${\displaystyle {}R/I}$ is a group and that the residue class mapping

${\displaystyle R\longrightarrow R/I,a\longmapsto a+I=:{\bar {a}},}$

is a group homomorphism. The only new feature compared with the group situation is that we now have also a multiplication. That the multiplication is well-defined can been seen as follows: Let two residue classes be given with different representatives, that is, ${\displaystyle {}{\overline {a}}\,={\overline {a'}}\,}$ and ${\displaystyle {}{\overline {b}}\,={\overline {b'}}\,}$. Then ${\displaystyle {}a-a'\in I}$ and ${\displaystyle {}b-b'\in I}$, and ${\displaystyle {}a'=a+x}$ and ${\displaystyle {}b'=b+y}$ with ${\displaystyle {}x,y\in I}$. This implies

${\displaystyle {}a'b'=(a+x)(b+y)=ab+ay+xb+xy\,.}$

The three summands on the right belong to the ideal, so that the difference ${\displaystyle {}a'b'-ab\in I}$. From the well-definedness, the other properties follows, in particular, that we have a ring homomorphism to the residue class ring. Again, this morphism is called the residue class mapping, or the residue class homomorphism. The image of ${\displaystyle {}a\in R}$ in ${\displaystyle {}R/I}$ is often denoted by ${\displaystyle {}[a]}$, ${\displaystyle {}{\bar {a}}}$, or just by ${\displaystyle {}a}$ again, and it is called the residue class of ${\displaystyle {}a}$. Under this mapping, exactly the elements from the ideal are sent to ${\displaystyle {}0}$, that is, the kernel of the residue class mapping is the given ideal.

The simplest example of this process is the mapping that sends an integer number ${\displaystyle {}a}$ to its remainder after division by a fixed number ${\displaystyle {}d}$. Every remainder is represented by one of the numbers ${\displaystyle {}0,1,2,\ldots ,d-1}$. In general, there does not always exist such a nice system of representatives.

The residue class rings of ${\displaystyle {}\mathbb {Z} }$

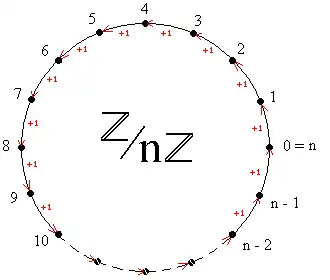
We know already the residue class groups ${\displaystyle {}\mathbb {Z} /(d)}$; they are cyclic groups of order ${\displaystyle {}d}$. Moreover, these groups get now also a ring structure.

Corollary

Let ${\displaystyle {}d\geq 0}$ be a natural number. Then there exists a uniquely determined ring structure on ${\displaystyle {}\mathbb {Z} /(d)}$ such that the residue class mapping

${\displaystyle \mathbb {Z} \longrightarrow \mathbb {Z} /(d),a\longmapsto {\overline {a}}\,,}$

is a ring homomorphism. ${\displaystyle {}\mathbb {Z} /(d)}$ is a commutative ring with ${\displaystyle {}d}$ elements (for

${\displaystyle {}d\geq 1}$).

Proof

This is a special case of the considerations above.

${\displaystyle \Box }$

Theorem

Let ${\displaystyle {}n\geq 1}$ be a natural number, and let ${\displaystyle {}\mathbb {Z} /(n)}$ be the corresponding residue class ring. Then the following statements are equivalent.

1. ${\displaystyle {}\mathbb {Z} /(n)}$ is a field.
2. ${\displaystyle {}\mathbb {Z} /(n)}$ is a domain.
3. ${\displaystyle {}n}$ is a prime number.

Proof

See Exercise 48.7 .

${\displaystyle \Box }$

The residue class rings ${\displaystyle {}S=K[X]/(P)}$ are also quite easy to understand (${\displaystyle {}K}$ a field). If ${\displaystyle {}P}$ has degree ${\displaystyle {}d}$, then every residue class in ${\displaystyle {}S}$ is represented by a unique polynomial of degree {{{1}}} This polynomial is the remainder that we get by dividing through ${\displaystyle {}P}$.

Orientations on a real vector space

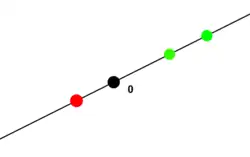
For a one-dimensional real vector space ${\displaystyle {}V}$ (s line), every vector ${\displaystyle {}\neq 0}$ is a base vector. If we remove the ${\displaystyle {}0}$, then the line splits into two halves (two half-lines, two rays). If the line is lying "horizontally“, then we talk about the left-hand and the right-hand side; but this concepts are problematic if we move the line or change the angle of view. However, it is a simple fact that there are two sides, and it is easy to determine whether two points belong to the same side or to different sides, even though it is difficult to put names on the two sides. The two points ${\displaystyle {}\neq 0}$ are related by their transformation matrix (base change matrix), which is just one real number. The two points lie on the same side if and only if their transformation matrix is positive, they lie on different sides if and only if their transformation matrix is negative.

In the plane, there is a similar phenomenon, the sense of rotation. If, for example, we want to walk around a tree on the earth, then we can do this clockwise or counter-clockwise. These notions are fixed by the convention that we look "from above“. For a mole in the ground, the sense of rotation is reversed. If we are given a plane in space, it is not at all clear what clockwise means. However, it is for every plane clear that there are two sense of rotation, and whether to such direction coincide. Also this phenomenon can be understood with bases and their transformation matrices. We consider the center of the clock as the origin of the plane, and the finger as a vector, depending on time. For two consecutive points in times ${\displaystyle {}t_{1}}$ and ${\displaystyle {}t_{2}}$, the finger represents the vectors ${\displaystyle {}v_{1}}$ and ${\displaystyle {}v_{2}}$, and we make sure that the finger has moved less than a half rotation. The vectors ${\displaystyle {}v_{1}}$ and ${\displaystyle {}v_{2}}$ define a basis in the plane (after a half rotation we had ${\displaystyle {}v_{2}=-v_{1}}$, and the vectors were linearly dependent). Suppose that at the start time ${\displaystyle {}t_{1}=0}$, the finger shows upstairs, then the clockwise motion of the finger is parametrized by ${\displaystyle {}{\begin{pmatrix}\sin t\\\cos t\end{pmatrix}}}$.. The two vectors are

${\displaystyle v_{1}={\begin{pmatrix}0\\1\end{pmatrix}},\,v_{2}={\begin{pmatrix}\sin t\\\cos t\end{pmatrix}}{\text{ with }}0<t<\pi .}$

The transformation matrix between the standard basis

${\displaystyle u_{1}={\begin{pmatrix}1\\0\end{pmatrix}},\,u_{2}={\begin{pmatrix}0\\1\end{pmatrix}}}$

is

${\displaystyle {}M_{\mathfrak {u}}^{\mathfrak {v}}={\begin{pmatrix}0&\sin t\\1&\cos t\end{pmatrix}}\,.}$

The determinant of this matrix is ${\displaystyle {}-\sin t}$, and this is negative for ${\displaystyle {}t}$ in the given range, for ${\displaystyle {}t}$ from ${\displaystyle {}]\pi ,2\pi [}$ it is positive. The transformation matrices between the bases

${\displaystyle v_{1}={\begin{pmatrix}0\\1\end{pmatrix}},\,v_{2}={\begin{pmatrix}\sin t\\\cos t\end{pmatrix}}{\text{ and }}w_{1}={\begin{pmatrix}0\\1\end{pmatrix}},\,w_{2}={\begin{pmatrix}\sin s\\\cos s\end{pmatrix}}{\text{ with }}t,s\in {]0,\pi [}}$

have a positive determinant. In this way, the clockwise direction does not fix a basis but it determines a class of bases with the property that their transformation matrix always has a positive determinant. For the counter-clockwise direction, we get bases of the type

${\displaystyle v_{1}={\begin{pmatrix}0\\1\end{pmatrix}},\,v_{2}={\begin{pmatrix}-\sin t\\\cos t\end{pmatrix}}{\text{ with }}t\in {]0,\pi [};}$

the transformation matrices of these bases to the standard basis have positive determinant.

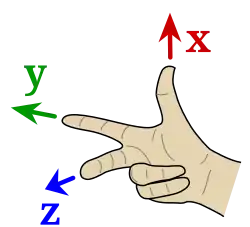
In space, there is a similar phenomenon; the human body helps to understand it. The right hand and the left hand are mirror-inverted (the leftt hand is the hand that is closer to the heart). We take a hand, we consider the center of the palm as the origin, and we stretch the thumb, the forefinger and the middle finger such that the thumb and the forefinger look like a pistol, and the middle finger points to the inside. The three fingers form in this ordering a sequence of three vectors in space, and they form a basis.

If we do this with the left hand and with the right hand, then it is possible to bring the thumbs and the forefingers in parallel position, but the middle fingers show in opposite direction. The transformation matrix between these two hand bases is

${\displaystyle {\begin{pmatrix}1&0&0\\0&1&0\\0&0&-1\end{pmatrix}},}$

its determinant is negative. The right hand and the left hand represent different orientations of space bases.

We give now the general definition of an orientation. In the following, it is important to recall that a basis is not a set of the basis vectors ${\displaystyle {}\{v_{1},\ldots ,v_{n}\}}$ but the ordered tuple ${\displaystyle {}(v_{1},\ldots ,v_{n})}$ of basis vectors.

This relation between bases is an equivalence relation; there are only two equivalence classes (called orientation or orientation classes) (with the exception of the zero space).

It is easy to determine whether two bases has the same of the opposite orientation; however, it does not make sense to give a name to each orientation.

A vector space becomes oriented by declaring that ${\displaystyle {}V}$ has the orientation represented by the basis ${\displaystyle {}v_{1},\ldots ,v_{n}}$. The standard space ${\displaystyle {}\mathbb {R} ^{n}}$ carries usually the so-called standard orientation, represented by the standard basis ${\displaystyle {}e_{1},\ldots ,e_{n}}$. The standard orientation of ${\displaystyle {}\mathbb {R} }$ is represented by ${\displaystyle {}1}$, and by every positive number. The standard orientation of ${\displaystyle {}\mathbb {R} ^{2}}$ corresponds, when we draw the first standard vector to the right, and the second standard vector perpendicular upstairs, to the counter-clockwise orientation. In space, the standard orientation corresponds to the right-hand rule, when the first axis goes to the right, the second axis to the back and the third axis upstairs. The right hand yields a human-natural orientation of the space we are living in, and the standard orientation yields an orientation on ${\displaystyle {}\mathbb {R} ^{3}}$; these two things are unrelated, as there are many way to establish a coordinate system. The coordinate system just mentioned rests on a convention.

On an arbitrary real vector space, there is no canonical way to mark an orientation. For every real finite-dimensional vector space a, there exist a bijective linear mapping

${\displaystyle \varphi \colon \mathbb {R} ^{n}\longrightarrow V,}$

and this sends the standard basis to a basis of ${\displaystyle {}V}$; however, this image basis and its orientation class depend on the chosen ${\displaystyle {}\varphi }$. It is not possible to define on every ${\displaystyle {}V}$ an orientation in a canonical way.

On a real affine space ${\displaystyle {}E}$, an orientation is just an orientation of the underlying real vector space.

Definition

Let ${\displaystyle {}V}$ and ${\displaystyle {}W}$ be finite-dimensional oriented real vector spaces. A bijective linear mapping

${\displaystyle \varphi \colon V\longrightarrow W}$

is called orientation-preserving, if for every basis ${\displaystyle {}v_{1},\ldots ,v_{n}}$ representing the orientation

on ${\displaystyle {}V}$, the image vectors ${\displaystyle {}\varphi (v_{1}),\ldots ,\varphi (v_{n})}$ represent the orientation on ${\displaystyle {}W}$.

It is enough to establish this property for just one basis representing the orientation; see Exercise 48.19 . For an automorphism ${\displaystyle {}\varphi \colon V\rightarrow V}$, we can directly talk about orientation-preserving, without declaring an orientation. We have an orientation-preserving linear mapping if and only if every basis ${\displaystyle {}v_{1},\ldots ,v_{n}}$ and its image basis ${\displaystyle {}\varphi (v_{1}),\ldots ,\varphi (v_{n})}$ have the same orientation. This follows from the following fact.

Lemma

Let ${\displaystyle {}V}$ be a finite-dimensional real vector space, and let ${\displaystyle {}\varphi \colon V\rightarrow V}$ denote a bijective linear mapping. Then ${\displaystyle {}\varphi }$ is orientation-preserving if and only if the determinant

of ${\displaystyle {}\varphi }$ is positive.

Proof

Let ${\displaystyle {}v_{1},\ldots ,v_{n}}$ be a basis of ${\displaystyle {}V}$. Because of the bijectivity of ${\displaystyle {}\varphi }$, the images

${\displaystyle \varphi (v_{1}),\ldots ,\varphi (v_{n})}$

form also a basis of ${\displaystyle {}V}$. Let

${\displaystyle {}\varphi (v_{j})=\sum _{i=1}^{n}a_{ij}v_{i}\,,}$

so that

${\displaystyle {}M={\left(a_{ij}\right)}_{ij}\,}$

is the describing matrix of the mapping with respect to the basis ${\displaystyle {}v_{1},\ldots ,v_{n}}$. This matrix is also the base change matrix ${\displaystyle {}M_{\mathfrak {v}}^{\mathfrak {\varphi (v)}}}$. The positivity of the determinant of this transformation matrix means by definition that the two matrices represent the same orientation.

${\displaystyle \Box }$

If ${\displaystyle {}V}$ is endowed with an inner product, and ${\displaystyle {}\varphi }$ is an isometry, then positive determinant means, due to Lemma 33.13 , that the determinant is ${\displaystyle {}1}$. Therefore, a proper isometry is the same as an orientation-preserving isometry.

Footnotes

1. ↑ For a ${\displaystyle {}0}$-dimensional vector space, that is, the zero space, we only have the empty basis. However, in some situations, it makes sense to talk about two orientations of the zero space, usually denoted by ${\displaystyle {}+}$ and ${\displaystyle {}-}$.