Linear algebra (Osnabrück 2024-2025)/Part II/Lecture 47

Commensurability

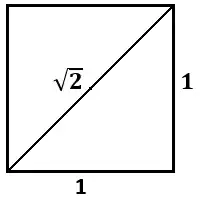
The side length and the diagonal in a square are not commensurable.

Definition

Two line segments ${}s$ und ${}t$

are called commensurable, if there exists a line segment

{}g

with the propery that both line segments are integer multiples of

{}g

The question, whether there exist, beside the rational numbers, further useful numbers, has its roots in ancient Greece. The question was raised in the form whether two lengths, given in a natural way, are always commensurable to each other (whether there exists a third length such that the two given lengths are integer multiples of it). The Pythagorean school believed in the harmony of the universe, and this implied that all proportions between natural lengths must be expressed by a proportion of integer numbers. They found such integer proportions in music (music intervals), and thought that such proportions hold for the motions of the planets, and for geometry in general. Some people speculate that they knew the reasoning of Fact ***** showing the irrationality of ${}{\sqrt {2}}$ (the incommensurability of the side length and the length of the diagonal in a square), but that they concealed this knowledge. Anyhow, later in ancient times the knowledge was accepted that there are irrational numbers.

The subgroup relation

{}(\mathbb {Q} ,0,+)\subseteq (\mathbb {R} ,0,+)\,

(which might be considered as a relation of a linear subspace of ${}\mathbb {Q}$ -vector spaces) yields also an equivalence relation on the real numbers. Here, two real numbers are equivalent if their difference is a rational number.

Homomorphism theorems

Theorem

Let ${}G,Q$ and ${}H$ be groups, and let ${}\varphi \colon G\rightarrow H$ be a group homomorphism and ${}\psi \colon G\rightarrow Q$ a surjective group homomorphism. Suppose that

{}\operatorname {kern} \psi \subseteq \operatorname {kern} \varphi \,.

ist. Then there exists a uniquely determined group homomorphism

{\tilde {\varphi }}\colon Q\longrightarrow H

such that ${}\varphi ={\tilde {\varphi }}\circ \psi$ holds. Put differently, the diagram

{\begin{matrix}G&{\stackrel {\varphi }{\longrightarrow }}&H&\\\!\!\!\!\!\psi \downarrow &\nearrow {\tilde {\varphi }}\!\!\!\!\!&\\Q&&&&\!\!\!\!\!\!\!\!\\\end{matrix}}

commutes.

Proof

We show firstly the uniqueness. For every Element ${}u\in Q$ , there exists some ${}g\in G$ with ${}\psi (g)=u$ . The commutativity of the diagram ensures that

{}{\tilde {\varphi }}(u)=\varphi (g)\,

holds. This means that there exists at most one ${}{\tilde {\varphi }}$ .

We have to show that this condition yields a well-defined mapping. Hence, let ${}g,g'\in G$ be two preimages of ${}u$ . Then

{}\psi {\left(g'g^{-1}\right)}=uu^{-1}=e_{Q}\,;

therefore, we have ${}g'g^{-1}\in \operatorname {kern} \psi \subseteq \operatorname {kern} \varphi$ . Hence, ${}\varphi (g)=\varphi (g')$ , and the mapping is well-defined. Let ${}u,v\in Q$ be given, and let ${}g,h\in G$ be preimages. Then ${}gh$ is a preimage of ${}uv$ . Therefore,

{}{\tilde {\varphi }}(uv)=\varphi (gh)=\varphi (g)\varphi (h)={\tilde {\varphi }}(u){\tilde {\varphi }}(v)\,.

This means that ${}{\tilde {\varphi }}$ is a group homomorphism.

\Box

Example

We consider the surjective group homomorphisms

\varphi \colon \mathbb {Z} \longrightarrow \mathbb {Z} /(4)

and

\psi \colon \mathbb {Z} \longrightarrow \mathbb {Z} /(12).

We have

{}\operatorname {kern} \psi =\mathbb {Z} \cdot 12\subseteq \mathbb {Z} \cdot 4=\operatorname {kern} \varphi \,.

Due to Theorem 47.4 , there exists a uniquely determined group homomorphism

{\tilde {\varphi }}\colon \mathbb {Z} /(12)\longrightarrow \mathbb {Z} /(4),

which is compatible with the remainder mappings. The morphism ${}{\tilde {\varphi }}$ sends the remainder of a number after division by ${}12$ to the remainder after division by ${}4$ . In particular, the theorem implies that the second remainder does only depend on the first remainder, not on the number itself.

If, to the contrary, we consider

\varphi \colon \mathbb {Z} \longrightarrow \mathbb {Z} /(5)

and

\psi \colon \mathbb {Z} \longrightarrow \mathbb {Z} /(12),

then

{}\operatorname {kern} \psi =\mathbb {Z} \cdot 12\not \subseteq \mathbb {Z} \cdot 5=\operatorname {kern} \varphi \,,

and there does not exists a natural mapping

\mathbb {Z} /(12)\longrightarrow \mathbb {Z} /(5).

For example, the numbers ${}1,13,25,37,49$ have modulo ${}12$ the remainder ${}1$ but modulo ${}5$ their remainders are ${}1,3,0,2,4$ .

The mapping constructed in this theorem is called induced mapping or induced homomorphism, and the theorem is called the theorem about the induced homomorphism.

Corollary

Let ${}G$ and ${}H$ be groups, and let

\varphi \colon G\longrightarrow H

be a surjective group homomorphism. Then there exists a canonical isomorphism

{\tilde {\varphi }}\colon G/\operatorname {kern} \varphi \longrightarrow H.

Proof

We apply Theorem 47.4 to ${}Q=G/\operatorname {kern} \varphi$ and the canonical projection ${}q\colon G\rightarrow G/\operatorname {kern} \varphi$ . This induces a group homomorphism

{\tilde {\varphi }}\colon G/\operatorname {kern} \varphi \longrightarrow H

fulfilling ${}\varphi ={\tilde {\varphi }}\circ q$ , which is surjective. Let ${}[x]\in G/\operatorname {kern} \varphi$ and ${}[x]\in \operatorname {kern} {\tilde {\varphi }}$ . Then

{}{\tilde {\varphi }}([x])=\varphi (x)=e_{H}\,.

Therefore, ${}x\in \operatorname {kern} \varphi$ . Hence, ${}[x]=e_{Q}$ , that is, the kernel of ${}{\tilde {\varphi }}$ is trivial, and so, due to Lemma 44.22 , ${}{\tilde {\varphi }}$ is also injective.

\Box

Example

Let ${}G$ be a cyclic group with a generator ${}g$ . We consider the corresponding group homomorphism

\varphi \colon \mathbb {Z} \longrightarrow G,n\longmapsto g^{n},

in the sense of Lemma 44.12 . Since we have a generator, this mapping is surjective. The kernel of this mapping is determined the order of ${}g$ , which we denote by ${}k$ (or it is ${}0$ , in case the order is ${}\infty$ ). Due to Corollary 47.6 , there exists a canonical isomorphism

{\tilde {\varphi }}\colon \mathbb {Z} /(k)\longrightarrow G.

In particular, there exists, up to isomorphism, for every ${}k$ , exactly one cyclic group, namely ${}\mathbb {Z} /(k)$ .

Example

The group homomorphism

\mathbb {R} \longrightarrow S^{1},t\longmapsto {\begin{pmatrix}\cos t\\\sin t\end{pmatrix}},

is surjective. Due to the periodicity of the trigonometric functions, the kernel equals ${}\mathbb {Z} 2\pi$ . By the isomorphism theorem, there exists a canonical isomorphism

{}\mathbb {R} /\mathbb {Z} 2\pi \cong S^{1}\,.

Example

The complex exponential function

(\mathbb {C} ,0,+)\longrightarrow (\mathbb {C} ^{\times },1,\cdot ),z\longmapsto \exp z,

is a surjective group homomorphism. The kernel is ${}\mathbb {Z} 2\pi {\mathrm {i} }$ . Due to the isomorphism theorem, there exists a canonical isomorphism

{}\mathbb {C} /\mathbb {Z} 2\pi {\mathrm {i} }\cong \mathbb {C} ^{\times }\,.

Example

The determinant

\det \colon \operatorname {GL} _{n}\!{\left(K\right)}\longrightarrow K^{\times },M\longmapsto \det M,

is a surjective group homomorphism; its kernel is by definition the special linear group ${}\operatorname {SL} _{n}\!{\left(K\right)}$ . Due to the isomorphism theorem, there exists a canonical isomorphism

{}\operatorname {GL} _{n}\!{\left(K\right)}/\operatorname {SL} _{n}\!{\left(K\right)}\cong K^{\times }\,.

Theorem

Let ${}G$ and ${}H$ be groups, and let

\varphi \colon G\longrightarrow H

be a group homomorphism. Then there exists a canonical factorization

G{\stackrel {q}{\longrightarrow }}G/\operatorname {kern} \varphi {\stackrel {\theta }{\longrightarrow }}\operatorname {Im} \varphi {\stackrel {\iota }{\hookrightarrow }}H,

where ${}q$ is the canonical projection, ${}\theta$ is a group isomorphism, and ${}\iota$ is the canonical inclusion of the

image group.

Proof

This follows from Corollary 47.6 , applied to the image group ${}U=\operatorname {Im} \varphi \subseteq H$ .

\Box

This statement is often briefly expressed by saying:

image ${}=$ preimage modulo kernel.

Theorem

Let ${}G$ be a group, and let ${}N\subseteq G$ be a normal subgroup with residue class group ${}Q=G/N$ . Let ${}H\subseteq G$ be another normal subgroup in ${}G$ with ${}N\subseteq H$ . Then the image ${}{\overline {H}}$ of ${}H$ in ${}Q$ is a normal subgroup, and we have a canonical isomorphism

{}G/H\cong Q/{\overline {H}}\,.

Proof

For the first statement, see Exercise 46.19 . Therefore, the residue class group ${}Q/{\overline {H}}$ is well-defined. We consider the composition

p\circ q:G\longrightarrow Q\longrightarrow Q/{\overline {H}}.

Because of

{}{\begin{aligned}\operatorname {kern} {\left(p\circ q\right)}&={\left\{x\in G\mid (p\circ q)(x)=e\right\}}\\&={\left\{x\in G\mid q(x)\in \operatorname {kern} p\right\}}\\&={\left\{x\in G\mid q(x)\in {\overline {H}}\right\}}\\&=H,\end{aligned}}

we have ${}\operatorname {kern} {\left(p\circ q\right)}=H$ . Hence, according to Corollary 47.6 , we get the canonical isomorphism

G/H\longrightarrow Q/{\overline {H}}.

\Box

In short, we have

{}G/H=(G/N)/(H/N)\,.

Residue class space

Lemma

Let ${}K$ be a field, let ${}V$ be a ${}K$ -vector space, and let ${}U\subseteq V$ denote a linear subspace. Then the relation given by

v\sim w,{\text{ if }}v-w\in U,

is an equivalence relation

on

{}V

.

Proof

This holds in general for the cosets of a subgroup, as was shown in the 46th lecture.

\Box

We give another direct proof that we have an a equivalence relation.

We look at the conditions of an equivalence relationn The reflexivity follows from ${}v-v=0\in U$ , the symmetry follows from ${}w-v=-(v-w)\in U$ . The transitivity follows like this: from ${}u-v\in U$ and ${}v-w\in U$ , we infer ${}u-w=(u-v)+(v-w)\in U$ .

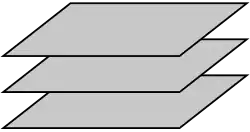
The cosets of a linear subspace ${}U$ have a simple geometric interpretation: a coset is nothing but an affine subspace of ${}V$ that is parallel to ${}U$ , that is, a space of the form ${}P+U$ with ${}P\in V$ . The quotient set is the set of these affine subspaces.

We may apply to this equivalence relation the general results for a normal subgroup in a group and the corresponding equivalence relation, and we obtain a surjective quotient mapping (or identifying mapping, or canonical projection)

q\colon V\longrightarrow V/\sim ,v\longmapsto q(v)=[v]=v+U.

instead of ${}V/\sim$ , we shall write ${}V/U$ . An extra feature in this situation is that this quotient set is itself a vector space, and that the canonical mapping is linear.

Theorem

Let ${}K$ be a field, let ${}V$ be a ${}K$ -vector space, and let ${}U\subseteq V$ denote a linear subspace. Let ${}V/U$ be the set of all equivalence classes (the quotient set) of the equivalence relation on ${}V$ defined by ${}U$ , and let

q\colon V\longrightarrow V/U,v\longmapsto [v],

denote the canonical projection. Then there exists a uniquely determined structure of a ${}K$ -vector space on ${}V/U$ such that ${}q$ is a

{}K

-linear mapping.

Proof

The existence and uniqueness of the group structure on ${}V/U$ , and the homomorphism property of the projection, follow from Theorem 46.14 . For the projection to be linear, the scalar multiplication must satisfy

{}\lambda [v]=[\lambda v]\,.

We have to show that by this condition, a well-defined scalar multiplication on ${}V/U$ is given. Let ${}v'=v+u$ , with ${}u\in U$ . Then we have

{}\lambda v'=\lambda (v+u)=\lambda v+\lambda u\,,

and the is equivalent to ${}\lambda v$ . The well-definedness of the scalar multiplication on ${}V/U$ and the surjectivity of the mapping imply that we have a vector space structure, and that the mapping is also compatible with the scalar multiplication.

\Box

Definition

Let ${}K$ be a field, let ${}V$ be a ${}K$ -vector space, and let ${}U\subseteq V$ denote a linear subspace. Then the set ${}V/U$ of all equivalence classes, together with the structure of a vector space as proven in Theorem 47.14 , is called the residue class space (or quotient space)

of

{}V

modulo

{}U

.

Theorem

Let ${}K$ be a field, and let ${}V,Q,$ and ${}W$ denote vector spaces over ${}K$ . Let ${}\varphi \colon V\rightarrow W$ be a linear mapping, and ${}\psi \colon V\rightarrow Q$ be a surjective linear mapping. Suppose that

{}\operatorname {kern} \psi \subseteq \operatorname {kern} \varphi \,

holds. Then there exists a uniquely determined linear mapping

{\tilde {\varphi }}\colon Q\longrightarrow W

fulfilling ${}\varphi ={\tilde {\varphi }}\circ \psi$ . In other words: the diagram

{\begin{matrix}V&{\stackrel {\varphi }{\longrightarrow }}&W&\\\!\!\!\!\!\,\,\psi \downarrow &\nearrow {\tilde {\varphi }}\!\!\!\!\!&\\Q&&&&\!\!\!\!\!\!\!\!\\\end{matrix}}

commutes.

Proof

The statement about existence and uniqueness follows from Theorem 47.4 . We have to show that the uniquly determined group homomorphism ${}{\tilde {\varphi }}$ is also compatible with scalar multiplication. Let ${}u\in Q$ be given with a preimage ${}v\in V$ , and let ${}\lambda \in K$ . Then ${}\lambda v$ is a preimage of ${}\lambda u$ ; therefore,

{}{\tilde {\varphi }}(\lambda u)=\varphi (\lambda v)=\lambda \varphi (v)=\lambda {\tilde {\varphi }}(u)\,,

and ${}{\tilde {\varphi }}$ is also compatible with the scalar multiplication.

\Box

The mapping ${}{\tilde {\varphi }}$ constructed in the preceding theorem is called the induced linear mapping; accordingly, the theorem is also called the theorem about the induced mapping.