Black-hole (Planck)

A Planck-unit black-hole universe CMB

The Planck hypersphere universe model describes a 4-axis incrementally (in Planck time units) expanding hypersphere universe (the bulk geometry), where the observable 3D universe exists on the surface. The fundamental premise is that particles exist on the 3D hypersphere surface and experience the physics described by ΛCDM, while the 4D bulk expansion follows Planck-scale geometric rules. The Planck universe can be considered as the scaffolding for the 3D particle universe, the method for addition of geometrical Planck units is discussed in the mathematical electron model.

It is found that the radiation component of the cosmic microwave background parameters shows a best fit for a 14.624 billion year old Planck unit universe (the radiation parameters are common to both Planck and ΛCDM cosmologies)^[1]. However the particle matter (observed universe) occurs only on the 3D surface, and as the ΛCDM cosmology occurs from observations of this hypersphere 3D surface, age for this surface is given at the lower 13.8 billion years as a consequence of time dilation.

It is offered that through coordinate transformations between the 4D bulk and 3D surface frames, ΛCDM density parameters can derived from hypersphere velocity components, and this is used to explain the discrepancies in age (both are correct). The model provides geometric interpretations for dark energy, establishes a fundamental connection between Casimir forces and CMB radiation, and offers potential resolution to cosmological tensions while maintaining compatibility with observational data ^[2].

The Planck hypersphere expands in Planck units per increment to the dimensionless incremental (universe age = 1, 2, 3, 4...), and this (constant) clock-rate is the only free parameter required in calculating the Planck cosmic microwave background.

The (dimensionless) universe clock-rate would be defined as the minimum discrete 'time variable' (t_age) increment to the universe. As an analogy to the programmed loop;

 'begin
 FOR tage = 1 TO the_end           //big bang = 1                 
         conduct certain processes ........ 
 NEXT tage                         //tage is an incrementing variable and not the dimensioned unit of time 
 'end 

For each increment to t_age, a set of Planck units (MLTA as geometrical objects) are added.

 FOR tage = 1 TO the_end                             
         generate Planck time T = tp       
         generate Planck mass M = mP      
         generate Planck volume (radius L = Planck length lp)     
         ........ 
 NEXT tage

As each t_age increment adds 1 unit of Planck time t_p, then in a 14 billion year old universe, numerically (note t_p has the units s, t_age is dimensionless)

t_age = t_p = 10⁶²

Comparison between the calculated Planck unit hypersphere and the ΛCDM parameters (table 1.).

Setting bh as the sum universe and t_sec as time measured in seconds;

${\displaystyle mass:\;m_{bh}=2t_{age}m_{P}}$

${\displaystyle volume:\;v_{bh}={\frac {4\pi r^{3}}{3}}\;\;\;(r=4l_{p}t_{age}=2ct_{sec})}$

${\displaystyle {\frac {m_{bh}}{v_{bh}}}={2t_{age}m_{P}}.\;{\frac {3}{4\pi {(4l_{p}t_{age})}^{3}}}={\frac {3m_{P}}{128\pi t_{age}^{2}l_{p}^{3}}}\;({\frac {kg}{m^{3}}})}$

Gravitation constant G in Planck units;

${\displaystyle G={\frac {c^{2}l_{p}}{m_{P}}}}$

${\displaystyle {\frac {m_{bh}}{v_{bh}}}={\frac {3}{32\pi t_{sec}^{2}G}}}$

From the Friedman equation; replacing p with the above mass density formula, √(λ) reduces to the radius of the universe;

${\displaystyle \lambda ={\frac {3c^{2}}{8\pi Gp}}=4c^{2}t_{sec}^{2}}$

${\displaystyle {\sqrt {\lambda }}=radius\;r=2ct_{sec}\;(m)}$

Measured in terms of Planck temperature T_P;

${\displaystyle T_{bh}={\frac {T_{P}}{8\pi {\sqrt {t_{age}}}}}\;(K)}$

The mass/volume formula uses t_age², the temperature formula uses √(t_age). We may therefore eliminate the age variable t_age and combine both formulas into a single constant of proportionality that resembles the radiation density constant.

${\displaystyle T_{p}={\frac {m_{P}c^{2}}{k_{B}}}={\sqrt {\frac {hc^{5}}{2\pi G{k_{B}}^{2}}}}}$

${\displaystyle {\frac {m_{bh}}{v_{bh}T_{bh}^{4}}}={\frac {2^{5}3\pi ^{3}m_{P}}{l_{p}^{3}T_{P}^{4}}}={\frac {2^{8}3\pi ^{6}k_{B}^{4}}{h^{3}c^{5}}}}$

From Stefan Boltzmann constant σ_SB

${\displaystyle \sigma _{SB}={\frac {2\pi ^{5}k_{B}^{4}}{15h^{3}c^{2}}}}$

${\displaystyle {\frac {4\sigma _{SB}}{c}}.T_{bh}^{4}={\frac {c^{2}}{1440\pi }}.{\frac {m_{bh}}{v_{bh}}}}$

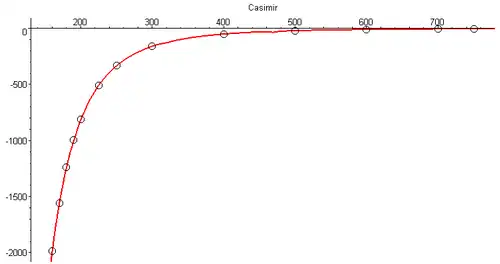
The Casimir force per unit area for idealized, perfectly conducting plates with vacuum between them; F = force, A = plate area, d_c 2 l_p = distance between plates in units of Planck length

${\displaystyle {-F_{c}}{A}={\frac {\pi hc}{480{(d_{c}2l_{p})}^{4}}}}$

if d_c = 2 π √t_age then the Casimir force equates to the radiation energy density formula.

${\displaystyle {\frac {-F_{c}}{A}}={\frac {c^{2}}{1440\pi }}.{\frac {m_{bh}}{v_{bh}}}}$

The diagram (right) plots Casimir length d_c2l_p against radiation energy density pressure measured in mPa for different t_age with a vertex around 1Pa. A radiation energy density pressure of 1Pa occurs around t_age = 0.8743 10⁵⁴ t_p (2987 years), with Casimir length = 189.89nm and temperature T_BH = 6034 K.

1 Mpc = 3.08567758 x 10²².

${\displaystyle H={\frac {1Mpc}{t_{sec}}}}$

${\displaystyle {\frac {xe^{x}}{e^{x}-1}}-3=0,x=2.821439372...}$

${\displaystyle f_{peak}={\frac {k_{B}T_{bh}x}{h}}={\frac {x}{8\pi ^{2}{\sqrt {t_{age}}}t_{p}}}}$

${\displaystyle S_{BH}=4\pi t_{age}^{2}k_{B}}$

Riess and Perlmutter using Type 1a supernovae to show that the universe is accelerating. This discovery provided the first direct evidence that Ω is non-zero giving the cosmological constant as ~ 10⁷¹ years;

${\displaystyle t_{end}\sim 1.7x10^{-121}\sim 0.588x10^{121}}$ units of Planck time;

This remarkable discovery has highlighted the question of why Ω has this unusually small value. So far, no explanations have been offered for the proximity of Ω to 1/t_univ² ~ 1.6 x 10^-122, where t_univ ~ 8 x 10⁶⁰ is the present expansion age of the universe in Planck time units. Attempts to explain why Ω ~ 1/t_univ² have relied upon ensembles of possible universes, in which all possible values of Ω are found ^[3] .

The maximum temperature T_max would be when t_age = 1. What is of equal importance is the minimum possible temperature T_min - that temperature 1 Planck unit above absolute zero, this temperature would signify the limit of expansion; t_age = the_end (the 'universe' could expand no further). For example, taking the inverse of Planck temperature;

${\displaystyle T_{min}\sim {\frac {1}{T_{max}}}\sim {\frac {8\pi }{T_{P}}}\sim 0.177\;10^{-30}\;K}$

This then gives us a value for the final age in units of Planck time (about 0.35 x 10⁷³ yrs);

${\displaystyle t_{end}=T_{max}^{4}\sim 1.014\;10^{123}}$

The mid way point (T_universe = 1K) would be when (about 108.77 billion years);

${\displaystyle t_{u}=T_{max}^{2}\sim 3.18\;10^{61}}$

${\displaystyle t_{Planck}}$ = 14.624 billion years

Age dilation:

${\displaystyle t_{\Lambda DCM}=t_{Planck}{\frac {v_{t}}{c}}}$ = 13.8 billion years

Hubble discrepancies (two different “frames”):

${\displaystyle H_{obs}=H_{4D}{\frac {v_{t}}{c}}}$

ΛCDM parameters from velocity-squared ratios:

${\displaystyle \sigma _{\Lambda }=({\frac {v_{t}}{c}})^{2}=(0.94365)^{2}}$ = 0.8905 (Tangential expansion energy)

${\displaystyle \sigma _{c}=({\frac {v_{r}}{c}})^{2}=(0.3309)^{2}}$ = 0.1095 (Radial gravitational energy)

${\displaystyle ({\frac {v_{t}}{c}})^{2}+({\frac {v_{r}}{c}})^{2}=1}$

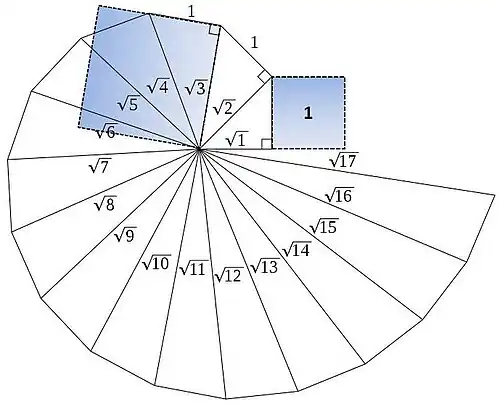
In this geometrical approach, the only free parameter used in the above calculations is the universe clock-rate. This clock-rate may also have geometrical origins rather than an externally imposed 'loop'. By expanding according to the geometry of the Spiral of Theodorus, where each triangle refers to 1 increment to t_age, we can map the mass and volume components as integral steps of t_age (the spiral circumference) and the radiation domain as a sqrt progression (the spiral arm). A spiral universe can rotate with respect to itself differentiating between an L and R universe without recourse to an external reference.

If mathematical constants are also a function of t_age, then their precision would depend on t_age, for example we can construct pi using this progression;

${\displaystyle {\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots }$

Mathematical constants may thus be naturally occurring, their accuracy improving as the universe ages.

https://chatgpt.com/share/683d0485-dc90-8012-b47f-6d3d27836ce9 
https://claude.ai/public/artifacts/fb6b2fe8-93f8-457a-a6db-40e464659f60
https://codingthecosmos.com/ai_pdf/Claude-Planck-LambdaCDM-06-2025.pdf
https://chat.qwen.ai/s/10b4edeb-39b7-4986-ba89-5d21109f00a9

Modelling using dimensionless geometrical forms derived from the universe clock-rate and 2 dimensionless physical constants (AI podcasts ^[4]).

• Electron_(mathematical): Mathematical electron from Planck units
• Planck_units_(geometrical): Planck units as geometrical forms
• Physical_constant_(anomaly): Anomalies in the physical constants
• Quantum_gravity_(Planck): Gravity at the Planck scale
• Fine-structure_constant_(spiral): Quantization via pi
• Relativity_(Planck): 4-axis hypersphere as origin of motion
• Black-hole_(Planck): CMB and Planck units
• Sqrt_Planck_momentum: Link between charge and mass

• The Simulation hypothesis
• Programming at the Planck scale using geometrical objects