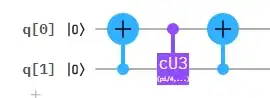
In section 3.3.2 of this PDF, The general SWAP gate is defined as
$ S (\alpha, \hat{y}) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos(\alpha/2) & -\sin(\alpha/2) & 0 \\ 0 & \sin(\alpha/2) & \cos(\alpha/2) & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} $
The same lecture notes claim that for $\alpha = \pi$, you get the SWAP gate. This is not correct if we perform the computation.
$ S (\pi, \hat{y}) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} $
Those lecture notes also say the square root of SWAP can be created by setting $\alpha=\frac{\pi}{2}$. When we do that we get
$ S (\frac{\pi}{2}, \hat{y}) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} $
The matrix for the square root of Swap is $ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \frac{1}{{2}} (1+i) & \frac{1}{{2}} (1-i) & 0 \\ 0 & \frac{1}{{2}} (1-i) & \frac{1}{{2}} (1+i) & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} $
This is not the same matrix as the one we get when we use the general SWAP matrix. Is the matrix for the general SWAP from those lecture notes correct? I haven't been able to find another source to cross-reference.