Why is implementation of controlled Hadamard on IBM Q so complex?

Question

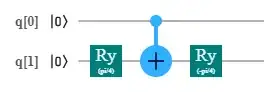
With reference to question how to implement CCH gate I easily realized that CH gate can be implemented with $\mathrm{Ry}$ gates and $\mathrm{CNOT}$ followingly:

Note $\theta = \frac{\pi}{4}$ for first $Ry$ gate and $\theta = -\frac{\pi}{4}$ for second one.

However, when I put $\mathrm{CH}$ gate implemented on IBM Q to circuit, a transpiled circuit has this form:

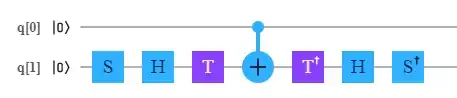
So, the first circuit has only two one qubit gates whereas the second one has six such gates. If I understand it correctly, any single qubit gate is on IBM Q eventually replaced by $\mathrm{U3}$ gate with respective parameters.

It seems to me that the second circuit is unnecessary complex.

Is there any reason why to implement $\mathrm{CH}$ gate in such way or am I missing something?

Answer 1

Summarization based on discussion with user met927:

• Transpiled circuit form depends on used backend - it is different for simulator and real quantum processor:
  • On simulator, the $\mathrm{CH}$ gate is transpiled to the circuit shown above
  • On real quantum processor, the gate is implemented with two $\mathrm{U2}$ gates and $\mathrm{CNOT}$ (i.e. like in the first figure in the answer)

Overall, the $\mathrm{CH}$ gate implementation on IBM Quantum is efficient.