How to implement the controlled square root of NOT gate on the IBM Q composer?

Question

I already know how to do that for Z, Y, and H gates. How can I make a controlled sqrt-of-NOT gate? I mean the controlled version of the gate described here.

Answer 1

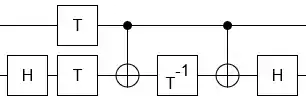
Here's one decomposition:

It was made by decomposing a controlled S (which is easier to think about because it only phases; it's diagonal) and then converting the basis of the target by conjugating with Hadamards.

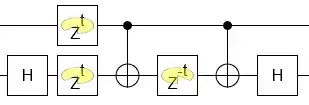
It generalizes in-place to any $\text{CNOT}^{2t}$:

Answer 2

I cannot add a comment, but I have a little question to the answer, sorry.

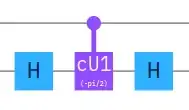
Why exactly $-\pi/2$ (with minus) is a parameter of the cU1 gate in your circuit? Isn't e.g. $\pi/2$ (without minus) appropriate?

Answer 3

If take e.g. this decomposition of the square root of NOT then it's so simple in the IBM Q composer:

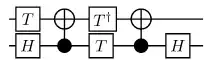
And although it is unlikely that this circuit form actually consists of 3 elementary gates (I think the cu1 gate is implemented using 5 elementary ones), in my opinion, it looks just easier than others e.g. from here:

You can also use functions (subroutines) in the composer (like as csx from qelib1.inc), but unfortunately they do not work well any time or work with restrictions.