Matrix representation of multiple qubit gates (Hadamard transform on single wire)

Question

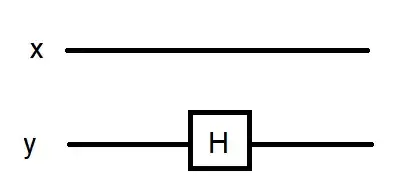
I would like to know how the unitary matrix for this circuit looks like:

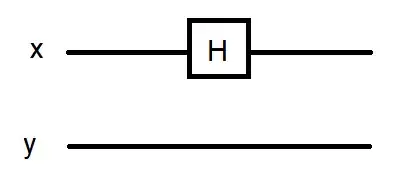
I'm not sure but I would try something like this:

First part:

$\begin{pmatrix}1&0\\0&0\end{pmatrix}\otimes H_1=\begin{pmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0&0\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0&0\\0&0&0&0\\0&0&0&0\end{pmatrix}$

Second part:

$\begin{pmatrix}0&0\\0&1\end{pmatrix}\otimes I_1=\begin{pmatrix}0&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}$

putting them together:

$\begin{pmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0&0\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0&0\\0&0&0&0\\0&0&0&0\end{pmatrix}+\begin{pmatrix}0&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}=\begin{pmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0&0\\\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}$

I'm not sure if that's right, that's just a consideration of mine.

Assuming the circuit would look like that, what does the matrix look like?

Answer 1

Your matrix representation is incorrect. In the first case, a $\mathbf H$ gate is applied to the first qubit $A$ and an identity gate $\Bbb I$ is applied to the second qubit $B$. So the effective quantum gate acting on the two-qubit system is $\mathbf H\otimes \Bbb I$. This is precisely because $(\mathbf H|0\rangle_A) \otimes (\Bbb I|0\rangle_B) = (\mathbf H\otimes \Bbb I)(|0\rangle_A \otimes |0\rangle_B)$ as explained here. Similarly, for the second case, the effective quantum gate is $\Bbb I\otimes \mathbf H$. If you know the matrix representations of $\mathbf H$ and $\Bbb I$, simply calculate the two Kronecker products, to get the corresponding matrix representations.