Is the set of all states with negative conditional Von Neumann entropy convex?

Question

I have read somewhere / heard that the set of all states that have non-negative conditional Von Neumann entropy forms a convex set. Is this true? Is there a proof for it?

Can anything be said about the reverse - set of all states that have negative conditional Von Neumann entropy?

Answer 1

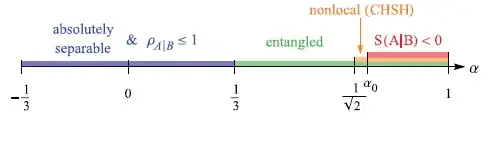
The conditional von Neumann entropy is a concave function: if $\rho$ and $\sigma$ are states of a pair of registers $(\mathsf{X},\mathsf{Y})$ and $\lambda\in[0,1]$ is a real number, then $$ \mathrm{H}(\mathsf{X}|\mathsf{Y})_{\lambda\rho + (1-\lambda)\sigma} \geq \lambda\, \mathrm{H}(\mathsf{X}|\mathsf{Y})_{\rho} + (1-\lambda)\,\mathrm{H}(\mathsf{X}|\mathsf{Y})_{\sigma}. $$ It follows that the set of all states having nonnegative conditional von Neumann entropy is convex. This is true for $\mathsf{X}$ and $\mathsf{Y}$ being registers with arbitrary dimension.

Some things can be said about the set of all states having negative conditional von Neumann entropy. Every such state is entangled, for instance, but it is certainly not a convex set.

One way to prove that the conditional von Neumann entropy is concave is as follows. Consider the state $$ \lambda\, \rho \otimes |0\rangle\langle 0| + (1-\lambda)\, \sigma \otimes |1\rangle\langle 1| $$ of three registers $(\mathsf{X},\mathsf{Y},\mathsf{Z})$, where $\mathsf{Z}$ is a new, single qubit register that is being introduced for the sake of the proof. By the strong subadditivity of von Neumann entropy we have $$ \mathrm{H}(\mathsf{X},\mathsf{Y},\mathsf{Z}) + \mathrm{H}(\mathsf{Y}) \leq \mathrm{H}(\mathsf{X},\mathsf{Y}) + \mathrm{H}(\mathsf{Y},\mathsf{Z}). $$ If you evaluate each of the entropies in this inequality for the state above, and then rearrange using $\mathrm{H}(\mathsf{X}|\mathsf{Y}) = \mathrm{H}(\mathsf{X},\mathsf{Y})-\mathrm{H}(\mathsf{Y})$, you should get the concavity of conditional von Neumann entropy.

Of course, the strong subadditivity of von Neumann entropy is far from trivial to prove, but there are multiple known proofs, and if you search you will easily find one.

Answer 2

Geometric characterization (as any other characterization) of subsets of the quantum state space in relation with their locality and entanglement properties becomes very complicated as the number of qubits rises. The geometry of the space of negative conditional entropy two qubit states, which are also locally maximally mixed (Weyl states) is known; it is reviewed by Friis, Bulusu and Bertlmann. All the figures and the data given in this answer are taken from this review.

Their result is described in the following figure of the Weyl tetrahedron, which can be summarized as follows:

1. The corners of the tetrahedron are the four Bell states.
2. The center of the tetrahedron is the maximally mixed two qubit sate.
3. The maximally mixed state is surrounded by what is called the Kuś-Życzkowski ball of maximally separable states whose unitary translates are also separable.
4. The surface of the ball touches the double pyramid of separable states in the central points of its faces.
5. The dark-yellow surface outside the double pyramid encloses the local states which cannot violate the CHSH inequality.
6. The outer red surface encloses all the states with positive conditional entropy.
7. The solid red line parametrizes a family of Werner states which penetrates through the whole Weyl tetrahedron. The cross section of this line in the tetrahedron is given by: