Building a matrix corresponding to the teleportation circuit

Question

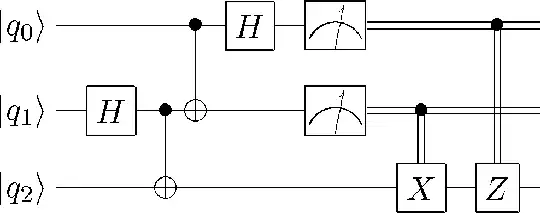
I'm trying to build the matrix that corresponds to this quantum teleportation circuit, but it never works when I test it in the quirk simulator, I tried finding the matrix corresponding to every part of the circuit and then multiplying but it never works, anyone knows what I might be doing wrong? When I was calculating the matrices I didn't consider the measurement gates.

Answer 1

Since the quantum teleportation circuit has three qbits, the matrix at each step is 8x8 and thus has 64 elements; this is pretty clunky to type out in its entirety, so I'll just walk you through step by step and you can derive the full matrix for a specific step if you want. Given a qbit we want to teleport:

$|\psi\rangle = \begin{bmatrix} \alpha \\ \beta \end{bmatrix}$

the operations are as follows:

$H_2C_{2,1}C_{1,0}H_1 \left ( \begin{bmatrix} \alpha \\ \beta \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0\end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0\end{bmatrix} \right ) = H_2C_{2,1}C_{1,0} \left ( \begin{bmatrix} \alpha \\ \beta \end{bmatrix} \otimes \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0\end{bmatrix} \right ) = H_2C_{2,1} \left (\begin{bmatrix} \alpha \\ \beta \end{bmatrix} \otimes \begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{2}} \end{bmatrix} \right ) = H_2 \left ( \frac{1}{\sqrt{2}} \begin{bmatrix} \alpha \\ 0 \\ 0 \\ \alpha \\ 0 \\ \beta \\ \beta \\ 0 \end{bmatrix} \right ) = \frac{1}{2} \begin{bmatrix} \alpha \\ \beta \\ \beta \\ \alpha \\ \alpha \\ -\beta \\ -\beta \\ \alpha \end{bmatrix}$

This is the vector directly before the first two qbits are measured. Note we can write it as follows:

$\frac{1}{2} \begin{bmatrix} \alpha \\ \beta \\ \beta \\ \alpha \\ \alpha \\ -\beta \\ -\beta \\ \alpha \end{bmatrix} = \frac{1}{2} \left ( |00\rangle \otimes \begin{bmatrix} \alpha \\ \beta \end{bmatrix} + |01\rangle \otimes \begin{bmatrix} \beta \\ \alpha \end{bmatrix} + |10\rangle \otimes \begin{bmatrix} \alpha \\ -\beta \end{bmatrix} + |11\rangle \otimes \begin{bmatrix} -\beta \\ \alpha \end{bmatrix} \right )$

We can then apply the intuitive "cancel and normalize" approach to measurement for each of the four possible measurement outcomes, which I outline in this answer. It should then become clear how applying the final $X$ and $Z$ gates (depending on measurement outcomes) will lead to the rightmost qbit taking on the value of $|\psi\rangle$.

If you'd like a more advanced account of how measurement works in quantum teleportation, you can also see an approach using the density operator which I go over here.