Implementation of Modular Exponentiation Function in Shor's Algorithm

Question

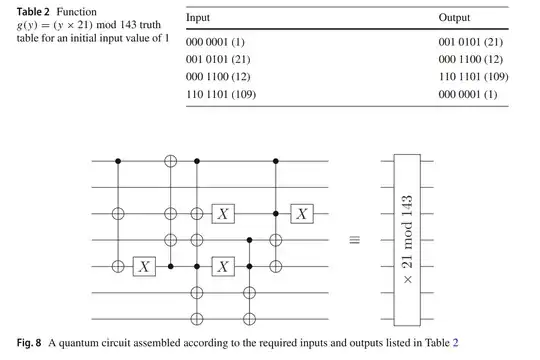
In this paper on the modular exponentiation function of Shor's Algorithm the author mentions creating a special circuit that decomposes the function $f(x)=a^x \mod N$ into

$$(...((a^{x_02^0} \mod N) \times a^{x_12^1} \mod N) \times ...) \times a^{x_{n-1}2^{n-1}} \mod N$$

inspired by other papers and Nielsen and Chuang Box 5.2, breaking up one modular exponentiation into a bunch of modular multiplications. So far, I understand this decomposition. Then, a new function $g(y) = (y \times a) \mod N$ is created an is used to mimic the nature of the modular exponentiation. For example: $$(y \times 21^2) \mod 143 = g(g(y)).$$ Next, a truth table is constructed, and a circuit is designed based on the truth table values. For example, my question is: does the circuit for this function merely check the values of the possible inputs listed in the truth table and transform them? if so, why does it work compared to the arithmetic computations seen in most approaches (e.g., example).

An example of the truth table and circuit:

Answer 1

To give a right-off-the-bat answer, it seems to me as if the circuit in Fig. 8 has been specially crafted to produce the correct results for the set $\{g^0, g^1, g^2, g^3\}$, where $g = 21 \in \mathbb Z_N^*$ and $N = 143$, whereas the circuit in [VBE96] is generic. More specifically, the specially crafted circuit exploits that $g$ has been selected to be of low order $r = 4$. (And if we already know this, then there is no point in performing order finding.)

You can see this yourself if you simulate the circuit in Fig. 8 using Quirk.