Specialized/hardcoded modular exponentiation circuit for Shor's

Question

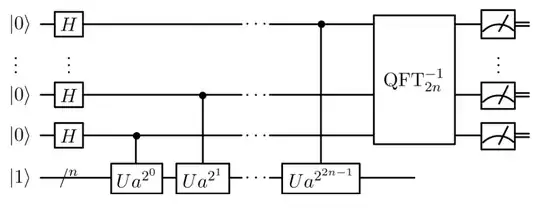
While researching to implement Shor's algorithm, I came across the following curcuit diagram (diagram 1).

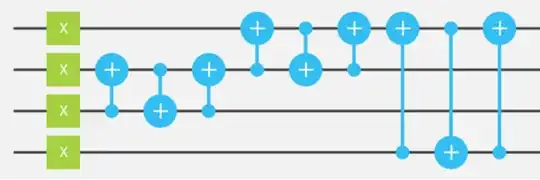
And while researching for how to implement the U operator, I came across the following circuit diagram (diagram 2).

The circuit in diagram 2 gives 'mod' outputs for $7^x\mod 15$ as follows: $$\ |1\rangle \text{ gives } |7\rangle$$ $$\ |7\rangle \text{ gives } |4\rangle$$ $$\ |4\rangle \text{ gives } |13\rangle$$ $$\ |13\rangle \text{ gives } |1\rangle$$ and it repeats after $4$ times with the period being $4$.

So here're my questions:

1. is the circuit in the diagram 2, the 'U' operator from diagram 1?
2. if yes, does that circuit need to be repeated those many times for every $Ua^k$ operator?
3. if yes, how to modify this circuit so it can be controlled by the superpositioned qubits from the circuit of diagram 1?

Thanks in advance.

Answer 1

1. is the circuit in the diagram 2, the $U$ operator from diagram 1?

Yes. Just keep in mind this circuit is a "cheat" since it only works as: $ U |y\rangle = |(7 \times y) \text{ mod } 15 \rangle$.

2. if yes, does that circuit need to be repeated those many times for every $Ua^{2^k}$ operator?

Yes. It needs to be repeated $2^k$ times for each $k^{\text{th}}$ application. Although, as pointed out in the comments below, for $ k \geq 2 $ the operator becomes the identity, so there is no need to apply those unitaries.

3. if yes, how to modify this circuit so it can be controlled by the superpositioned qubits from the circuit of diagram 1?

You will have to take each gate of this circuit and condition it based on the qubit you want to control it by. However, most quantum SDKs will let you define this circuit as a "block" or "gate", and then condition that gate based on the qubit of interest.