I am new to quantum computing. I want to find out the circuit depth of the following circuit.
In the circuit, one $\mathcal{ADD}$ operator has 154 CNOT gates and 216 Toffoli gates. The $\mathcal{RL}$ does not have any gate inside it. It is a rotation operator.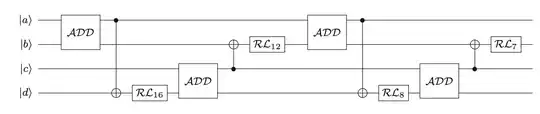
If I assume the $\mathcal{ADD}$ operator as a gate itself, then is the depth 9 as for register $|d\rangle$ it is 9 ? Also if I consider the CNOT gates and Toffoli gates, what will be the depth of the circuit ?
I am having hard time understand the full depth of the circuit. Can anyone please help or guide me how to do would have been of great help. Thank you.