0

Quantum teleportation for single qubit is a fairly simple algorithm to follow. Even its extensions into the transportation of $n$ qubits is fairly simple: repeat the process $n$ times (or run $n$ iterations simultaneously), as seen here.

I'm looking for an algorithm for transporting an entangled state in $H^{\otimes n}$.

To take the (presumably) simple case, let us say I want to teleport $\alpha|00\rangle+\beta|11\rangle$ to another party. I do not know the coefficients. How would I go about doing it? Having a circuit representation would be ideal.

Once that is covered, what about the quantum teleportation of an unknown state entangled over $n$ qubits?

Alan Whitteaker
  • 148
  • 9

2 Answers2

2

As mentioned in the link shared the the OP, a simple way to extend the teleportation protocol to $n$ qubits is to basically replicate the teleportation procedure for each of the qubits. This works even if the state to be teleported is entangled.

However, for sake of clarity, I am posting a separate answer here since the example given in the original post is specifically for 2 qubits, uses deferred measurements, and shows the answer in terms of measured probabilities, which is not a guarantee that the state was teleported with the correct phases.

The Qiskit code below works for an arbitrary number of $n$ qubits. The only adjustment needed is to make sure the list used to define the state ψ is of size $2^n$ and represents the normalized probability amplitudes of a valid statevector.

# imports

import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile
from qiskit.quantum_info import Statevector, partial_trace
from qiskit_aer import AerSimulator


Number of qubits


n = 3


Arbitrary amplitudes to prepare state |ψ⟩ = α|001⟩ + β|010⟩ + γ|100⟩


α = np.sqrt(1/6)
β = np.sqrt(2/6)
γ = np.sqrt(3/6)


Prepare arbitrary state vector


ψ = [0,α,β,0,γ,0,0,0]


Define quantum registers


qrA = QuantumRegister(n, name="A")
qrE = QuantumRegister(n, name="E")
qrB = QuantumRegister(n, name="B")


Define classical register


cr = ClassicalRegister(2*n, name='M')


Compose quantum circuit


qc = QuantumCircuit(qrB, qrE, qrA, cr)
qc.prepare_state(ψ,qrA, label="$| \psi \rangle$")


qc.save_statevector('ψin')


for i in reversed(range(n)):
    qc.h(qrE[i])
    qc.cx(qrE[i],qrB[i])


qc.barrier()


for i in reversed(range(n)):
    qc.cx(qrA[i],qrE[i])
    qc.h(qrA[i])


qc.barrier()

qc.measure(qrE,cr[0:n])
qc.measure(qrA,cr[n:2*n])


for i in range(2*n):
    if i < n:
        qc.x(qrB[i]).c_if(i,1)
    else:
        qc.z(qrB[i-n]).c_if(i,1)


qc.save_statevector('ψout')


Transpile circuit


sim = AerSimulator()
qc_t = transpile(qc, sim)


Run Sim


result = sim.run(qc_t).result()


Extract Statevectors


ψin = result.data().get('ψin')
ψout = result.data().get('ψout')


Trace out syndrome qubits


ρin = partial_trace(ψin,range(0,2n))
ρout = partial_trace(ψout,range(n,3n))


transform back to statevector


ψin = ρin.to_statevector()
ψout = ρout.to_statevector()


print('State prepared by Alice:')
display(ψin)
print('State received by Bob:')
display(ψout)

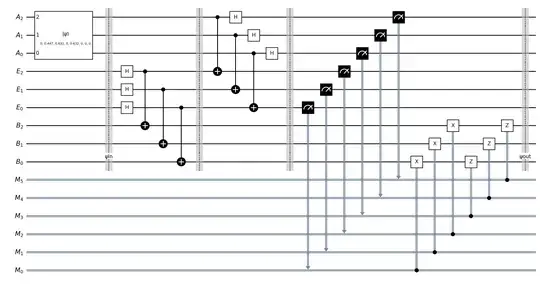
This code produces the following circuit to teleport 3 qubits: enter image description here

and generates the following output, which shows that the state Bob receives matches the state Alice prepared:

State prepared by Alice:

$ \frac{\sqrt{6}}{6} |001\rangle+\frac{\sqrt{3}}{3} |010\rangle+\frac{\sqrt{2}}{2} |100\rangle $

State received by Bob:

$ \frac{\sqrt{6}}{6} |001\rangle+\frac{\sqrt{3}}{3} |010\rangle+\frac{\sqrt{2}}{2} |100\rangle $

diemilio
  • 3,043
  • 1
  • 6
  • 16
1

Teleportation does not break entanglement. That means that for a general entangled state over $n$ qubits $$ (\alpha \left|{\psi}\right\rangle\otimes\left|{0}\right\rangle + \beta \left|{\psi'}\right\rangle\otimes\left|{1}\right\rangle)_A \underset{\text{Teleportation}}{\longrightarrow} \alpha \left|{\psi}\right\rangle_A \otimes\left|{0}\right\rangle_B + \beta \left|{\psi'}\right\rangle_A \otimes\left|{1}\right\rangle_B $$ with $\left|{\psi}\right\rangle$ and $\left|{\psi'}\right\rangle$ being an $n-1$ qubit state.

Perform this $n$ times and you can transfer any state in $H^{\otimes n}$.

Shoham Jacoby
  • 302
  • 6