Can we realize the index shift in a quantum circuit as we do in a classic circuit?
$\forall$ $a,b,c \in \{0,1\}$, $\left|abc\right>\mapsto\left|bca\right>$
e.g. $\left|001\right>\mapsto \left|010\right>$, $\left|010\right>\mapsto \left|100\right>$, and $\left|100\right> \mapsto \left|001\right>$
All qubit rearrangements can be implemented with two layers of swap gates. In the case of a shift operation, swap qubit $k$ with qubit $n-k-1$ for each $k < n/2$ then swap qubit $k+1$ with qubit $n-k-1$ for each $k+1 < n/2$.
I'll try to extend on @Jezer's answer. Although the obvious answer is the staircase product of SWAP operators $$S = \prod_{i=1}^{n-1} SWAP_{i,i+1},$$ it is most certainly more resource efficient to relabel the qubits, if $S$ is used in a larger quantum circuit. Suppose, you are doing a circuit $U_1$, then $S$, then a circuit $U_2$ and finally measure an observable $O$. Starting with $|0...0\rangle$, you will be measuring the expectation value $$\langle 0...0| U_1^\dagger S^\dagger U_2^\dagger O U_2 S U_1 | 0...0 \rangle = \langle 0...0| U_1^\dagger (S^\dagger U_2^\dagger S) (S^\dagger O S) (S^\dagger U_2 S) U_1 | 0...0 \rangle = \langle 0...0| (S U_1^\dagger S^\dagger) U_2^\dagger O U_2 (S U_1 S^\dagger) | 0...0 \rangle.$$ In the last equality, I used $S|0...0\rangle = |0...0\rangle$. The circuits/observables in brackets will not come with a resource overhead, as you can easily implement them by just shifting all gates/measurements by one qubit to the right ($S^\dagger XS$) or left ($SXS^\dagger$) respectively.
So if you are planning on doing a bit shift in a quantum circuit, don't implement $S$, use the trick!
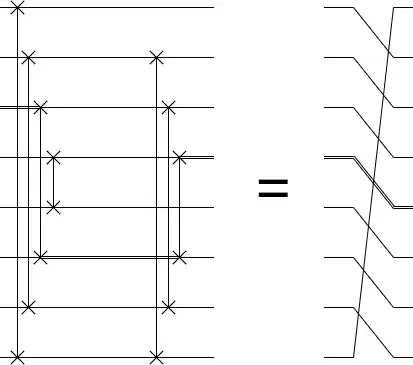
CW because this is mostly cumulative with the other answers
As the other answers explain, a ladder of SWAP gates should suffice to perform such a circular shift operation. Many times it would not make sense to have specific quantum gates implementing these SWAPs and it's much easier to just relabel the qubits.
However, often may you wish to have a "controlled shift", where the shifting is conditioned on another qubit. If this other qubit is ever in superposition, the relabeling trick won't help much.
For example, here is a Quirk circuit for doing a left-rotation controlled on the top qubit, which is in a superposition:
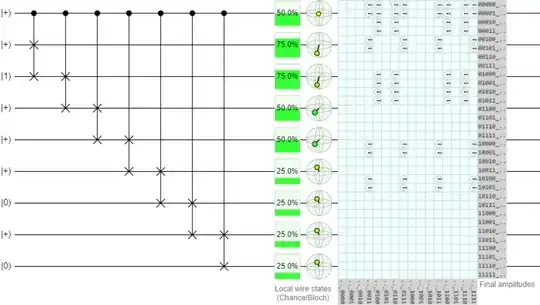
There is some analogy here to classical assembly language instructions. For example, the x86 instruction set includes ror 1, %ax and rol 1, %ax to cyclically rotate left and right the AX register by a single bit. This is a reversable operation. However, there is no corresponding way to have a quantum computer perform a shl or a shr instructions to shift a register to the left or right (to multiply or divide by 2), because such an instruction is not reversible as bits fall off the bit-bucket.
You could implement this with SWAP gates. Apply a SWAP on qubits 0 and 1, then on qubits 1 and 2, and so on, till you finally SWAP qubits n-1 and n.
If however, you're interested in designing algorithms and worry about the depth complexity of your circuit in theory, you might want to just relabel your qubits and build the rest of your circuit accordingly.
