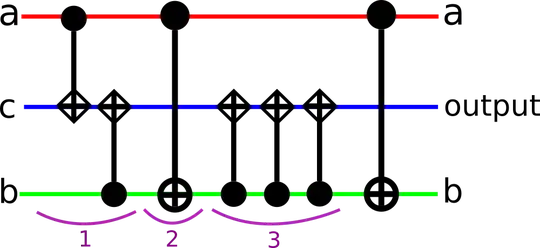
In Quantum Computation with the simplest maths possible there is a section titled "Doing maths with a controlled-half NOT" which covers a reversible-(N)AND circuit with controlled-half NOTs.
What would the unitary matrix for a controlled-half NOT be?
How could a reversible-XNOR gate be constructed with controlled-half NOTs?
How would a half-adders, full adders & ripple carry adders be constructed from controlled-half NOTs?
This is the gate that I would call controlled-square-root-of-not. Bit more of a mouthful, I know, but perhaps conveys more accurately what it's doing. The point is that it's a unitary $U$ such that $U^2$ is the controlled-not. There are probably a few ways of writing down such a thing, but, for example $$ U=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \frac{e^{i\pi/4}}{\sqrt{2}} & \frac{e^{-i\pi/4}}{\sqrt{2}} \\ 0 & 0 & \frac{e^{-i\pi/4}}{\sqrt{2}} & \frac{e^{i\pi/4}}{\sqrt{2}} \end{array}\right) $$
There's a trivial answer to your other questions. Take the normal circuits for each of these things built out of (n)and gates, and substitute the reversible (n)and circuits in their place. Of course, there may be optimisations to improve things slightly...
