What is the minimum number of non-Clifford gates does it take to prepare a superposition over all "two-hot" basis vectors?

Question

The generalized W state:

$$W_n=\frac{1}{\sqrt{n}}(|100\cdots 0\rangle + |010\cdots 0\rangle + \ldots + |00\cdots 01\rangle)$$

is often thought of as the uniform superposition over all "one-hot" basis vectors, as each such vector has a single qubit in the $|1\rangle$ state with all others in the $|0\rangle$ state.

Reviewing this question it appears that the generalized W state on $n$ qubits can be prepare from the all-zeroes ket with roughly a linear number of non-Clifford gates. This is in some contrast to the generalized GHZ state/cat state, which can similarly be prepared but only with a single Hadamard and a linear number of CNOT/SWAP gates.

In considering this question I proposed that a generalized superposition over all "two-hot" basis states, e.g.:

$$\frac{1}{\sqrt{n(n-1)/2}}(|1100\cdots 0\rangle + |1010\cdots 0\rangle + \ldots + |0\cdots 0011\rangle)$$

may require a quadratic number of non-Clifford gates to prepare, starting from the all-zeroes ket. My intuition is that there are $n\choose 2$ such states, and accordingly there may be a quadratic number of gates required.

Is this guess correct? In general, does it take a minimum of roughly $n\choose k$ gates to prepare a uniform superposition of all "$k$-hot" vectors on $n$ qubits, starting from some canonical state such as the all-zeroes ket?

This question is borne out of idle curiosity more than anything, to be honest, but it is perhaps interesting to ponder simple states that are a bit hard - but not too hard - to prepare, especially now in the NISQ era where generalized GHZ states are often prepared as test cases, as they are the most sensitive to decoherence, but such cat states can nonetheless be produced with "easier" Clifford gates.

EDIT

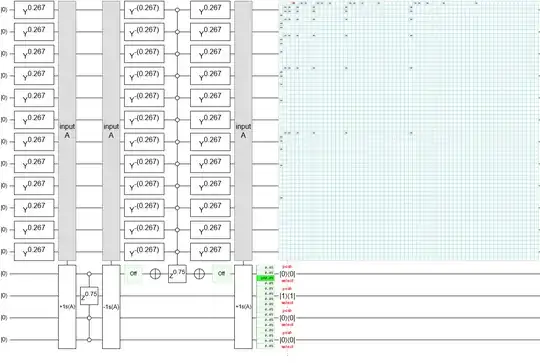
Hmmm... it appears that what I call the "$k$-hot" state is also known as a Dicke state. In "Deterministic Preparation of Dicke States" by Andreas Bärtschi and Stephan Eidenbenz can prepare just such a state with only $O(nk)$ gates. This Quirk circuit from their paper gives the $3$-hot Dicke state on five qubits.

Answer 1

This can be done efficiently by using amplitude amplification.

We are going to want to rotate each qubit such that it has a $2/n$ chance of being ON. For that it helps to have this class of gates:

$\text{Odds}_{a:b} = \begin{bmatrix}\sqrt{\frac{a}{a+b}} & -\sqrt{\frac{b}{a+b}} \\ \sqrt{\frac{b}{a+b}} & \sqrt{\frac{a}{a+b}}\end{bmatrix}$.

First step is to initialize all qubits to $|0\rangle$ and apply $\text{Odds}_{2:n-2}$ to every qubit.

If we were to measure the population count of the qubits at this point, and get a result of 2, then we would be done. The chance of that occurring approaches $2/e^2 \approx 25\%$ as $n$ increases. So it would be a perfectly acceptable repeat-until-success strategy to do it that way, with an expected non-Clifford count of $8n$ ($n$ from the odds gates, $n$ from the Hamming weight measurement, and a factor of 4 from the retries).

Instead of doing that, we are going to phase the states that have hamming weight 2 by around 135 degrees, apply $\text{Odds}_{2:n-2}^{-1}$ to every qubit, phase the $|0\rangle$ state by around 135 degrees, and apply $\text{Odds}_{2:n-2}$ to every qubit. This isn't exactly amplitude amplification, but it seems to work pretty well.

After these steps the overlap with $\left|{n \atop 2}\right\rangle$ is above 99%. I think you can get as close as you want to 100% by more carefully tuning that 135 degree rotation. It should limit to some specific angle as $n$ increases. Regardless, being above 99% is more than good enough to retry until success.

So now the expected non-Clifford count is $6.06n$, with $3n$ coming from the three layers of odds gates, $2n$ coming from the two times we had to compute the population count (once to phase it and once to postselect on it), $1n$ coming from phasing $|000...0\rangle$, and the last $0.06n$ coming from retries.

A particularly nice property of this construction is that the $6.06n$ non-Clifford gates can be all be Toffoli gates, instead of arbitrarily complex or accurate non-Clifford gates that are hard to distill. For this to work you'd pre-pay $O(\lg^2 \frac{1}{\epsilon})$ T gates to prepare phase gradient registers used for Hamming weight phasing.

Here's a quirk circuit showing it works: