Postponing post-processing through state injection protocols

Question

I am trying to build a $T$ injecton protocol and study how an $X^b$ post-process, supposed to happen before the protocol, behaves if delayed after the protocol.

The first example comes from the combination of the two protocols of figure 2. from this paper.

The result is something like this. Where I deferred and removed the measurements. It seems catalytic.

An alternative comes from this slide. Which, without measurements, looks like this.

To conclude, my question is: Assuming an $X^b$ operation at the beginning of a protocol. What it the equivalent operation that post-pone the correction?

Answer 1

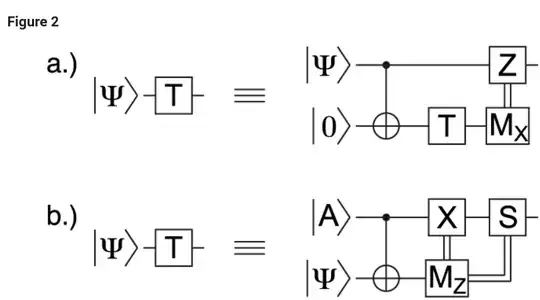
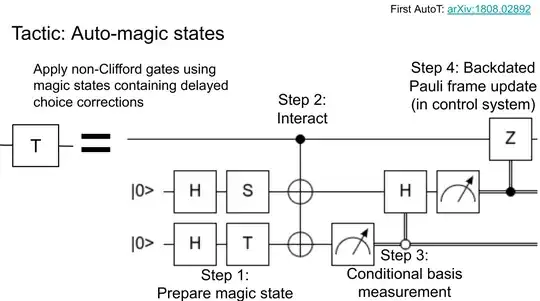
One of the nice things about using gate teleportation to implement non-Clifford gates is that the measurement that occurs during the teleportation helps propagate Pauli products through the construction.

Z always propagates right through a T gate so no need to worry about that one, let's focus on X.

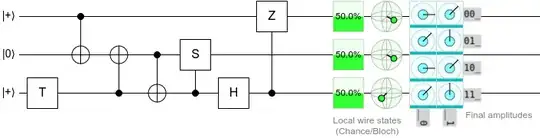
If the measurement returns 0, then an X propagates through like this:

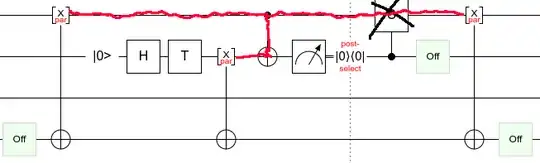
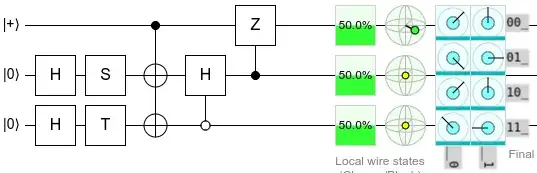
If the measurement returns 1, then an X propagates through like this:

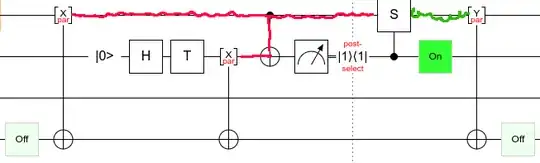
The qubit along the bottom is just there to verify I didn't make a mistake (if I screwed it up it wouldn't end up off). The coloring shows how the Pauli propagates through the system with X=red Y=green Z=blue.

There are two complications here. First, the propagation depends on the measurement result. This means that you are unable to relate Paulis after the gadget to Paulis before the gadget until you've processed the measurement result.

Second, there's that X dependence on the T state. This is where the non-cliffordness is coming from. The way you deal with this depends on what you are using the Pauli analysis for. If the Pauli propagation corresponds to the history of a logical observable, used to determine whether it was flipped by noise, then effectively this history terminates on a bootstrapping assumption that the physical T state injection+distillation succeeded. You always need some kind of special case to deal with this X dependence on T.

In general, you will find there is no way to turn any Pauli product before into always-a-Pauli-product after, because the whole point of these gadgets is to do non-Clifford operations and non-Clifford operations don't have the property that they conjugate Pauli products into Pauli products. The best you can do is limit the scope of the damage, such as limiting it to X dependence on T states.