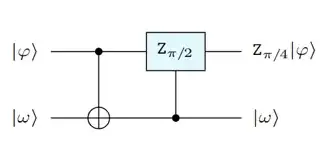
I found the protocol in figure on internet, without proof.
Here, $|\omega\rangle = TH|0\rangle$.
It is refered as catalytic injection. I doubt its correctness on the second qubit as it outputs $|\omega\rangle$, no matter what $|\varphi\rangle$ is.
Is it correct?
Let us denote $|\varphi\rangle$ as: $$|\varphi\rangle=a|0\rangle+b|1\rangle$$ Thus, the system starts in the state: $$(a|0\rangle+b|1\rangle)\otimes\frac{1}{\sqrt{2}}(|0\rangle+\mathrm{e}^{\mathrm{i}\frac\pi4}|1\rangle)=\frac{a}{\sqrt{2}}|00\rangle+\frac{a}{\sqrt{2}}\mathrm{e}^{\mathrm{i}\frac\pi4}|01\rangle+\frac{b}{\sqrt{2}}|10\rangle+\frac{b}{\sqrt{2}}\mathrm{e}^{\mathrm{i}\frac\pi4}|11\rangle$$ After having applied the first CNOT, the resulting state is: $$\frac{a}{\sqrt{2}}|00\rangle+\frac{a}{\sqrt{2}}\mathrm{e}^{\mathrm{i}\frac\pi4}|01\rangle+\frac{b}{\sqrt{2}}\mathrm{e}^{\mathrm{i}\frac\pi4}|10\rangle+\frac{b}{\sqrt{2}}|11\rangle$$ We then apply the controlled-$S$ (note that this means applying a phase of $\frac\pi2$ to the state where both qubits are in state $1$): $$\frac{a}{\sqrt{2}}|00\rangle+\frac{a}{\sqrt{2}}\mathrm{e}^{\mathrm{i}\frac\pi4}|01\rangle+\frac{b}{\sqrt{2}}\mathrm{e}^{\mathrm{i}\frac\pi4}|10\rangle+\frac{b}{\sqrt{2}}\mathrm{e}^{\mathrm{i}\frac\pi2}|11\rangle=\left(a|0\rangle+b\mathrm{e}^{\mathrm{i}\frac\pi4}|1\rangle\right)\otimes\frac{1}{\sqrt{2}}(|0\rangle+\mathrm{e}^{\mathrm{i}\frac\pi4}|1\rangle)=T|\varphi\rangle\otimes|\omega\rangle$$ Thus, this circuit is valid.
This is equivalent to the usual circuit by the deferred measurement principle:
You can also see why it works by decomposing the CS gate into CNOT+T:
