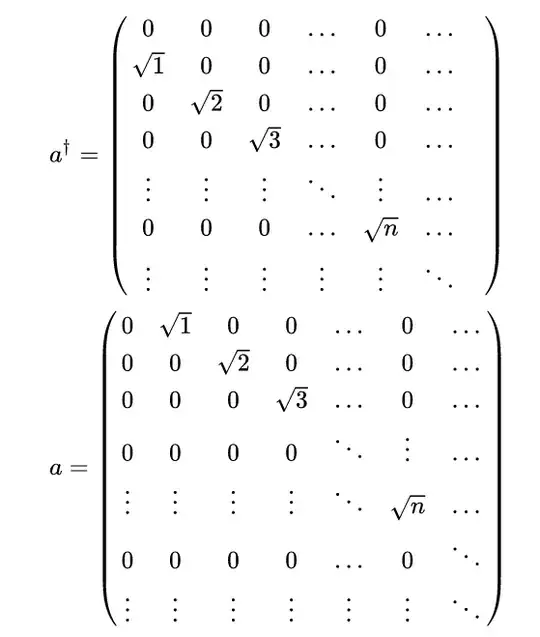
Background
Often, in quantum optics, the Heisenberg picture is used, where instead of considering equations of motion of states, equations of motions of operators are looked at instead. When considering creation/annihilation operators, this is often considerably easier as the matrices that determine the evolution (assuming it can be written in terms of matrices) are, for one, finite.
The Heisenberg equations of motions are calculated using $$\frac{dA}{dt} = \frac i\hbar \left[H, A\right] + \frac{\partial A}{\partial t},$$ for an operator $A$ evolving under a Hamiltonian $H$.
Here, the operator $a_j \left(a_j^\dagger\right)$ is the annihilation (creation) operator for spatial mode $j$. For a single mode, this allows for an effective Hamiltonian (acting on the operators) to be written as $$i\frac{d}{dt}\begin{pmatrix}a \\ a^\dagger\end{pmatrix} = H_{\text{eff}}\begin{pmatrix}a \\ a^\dagger\end{pmatrix}.$$ This naturally extends to writing their transformation as $$\begin{pmatrix}b \\ b^\dagger\end{pmatrix} = M\begin{pmatrix}a \\ a^\dagger\end{pmatrix}$$ for input modes $a \left(a^\dagger\right)$ and output modes $b \left(b^\dagger\right)$.
When it exists, this transformation matrix $M$ can be calculated using $U^\dagger A_jU = \sum_{k}M_{jk}A_k$ for unitary evolution $U$. For the Unitaries in the question, this gives:
Transformations
Displacement
$$D_j\left(\alpha\right):\begin{pmatrix}b_j\\b_j^\dagger\\I\end{pmatrix} = \begin{pmatrix}1 && 0 && \alpha\\0&&1&&\alpha^*\\0&&0&&1\end{pmatrix} \begin{pmatrix}a_j\\a_j^\dagger\\I\end{pmatrix}$$
Rotation
$$R_j\left(\phi\right):\begin{pmatrix}b_j\\b_j^\dagger\end{pmatrix} = \begin{pmatrix}e^{-i\phi} && 0\\0&&e^{i\phi}\end{pmatrix} \begin{pmatrix}a_j\\a_j^\dagger\end{pmatrix}$$
Squeezing
$$S_j\left(\xi=re^{i\theta}\right):\begin{pmatrix}b_j\\b_j^\dagger\end{pmatrix} = \begin{pmatrix}\cosh r && -e^{i\theta}\sinh r\\-e^{-i\theta}\sinh r&&\cosh r\end{pmatrix} \begin{pmatrix}a_j\\a_j^\dagger\end{pmatrix}$$
Beamsplitter
$$B_{jk}\left(\zeta = te^{i\varphi}\right):\begin{pmatrix}b_j\\b_k\\b_j^\dagger\\b_k^\dagger\end{pmatrix} = \begin{pmatrix}t && re^{-i\varphi}&&0&& 0\\re^{i\varphi}&&t&&0&&0\\0&&0&&t&&re^{i\varphi}\\0&&0&&re^{-i\varphi}&&t\end{pmatrix} \begin{pmatrix}a_j\\a_k\\a_j^\dagger\\a_k^\dagger\end{pmatrix},$$ where $r=\cos\left|\zeta\right|$.
Cubic Phase
Unfortunately, this is too nonlinear to write in the above way in matrix form. As $x = \frac{1}{\sqrt 2}\left(a+a^\dagger\right)$, even to first order, $V^\dagger a^\dagger V$ will include terms such as $\left[a^3, a^\dagger\right] = 3a^2$, which cannot be written in terms of $\alpha a^\dagger+\beta a+\gamma$.