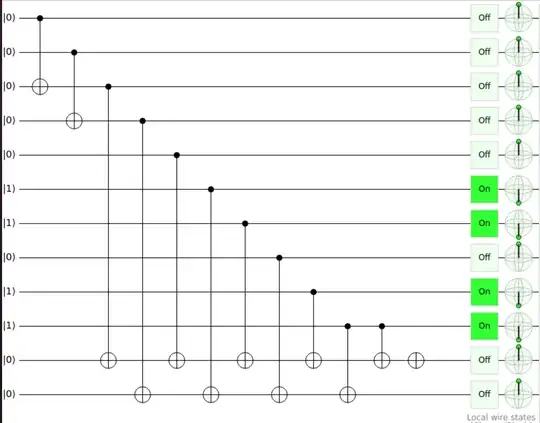
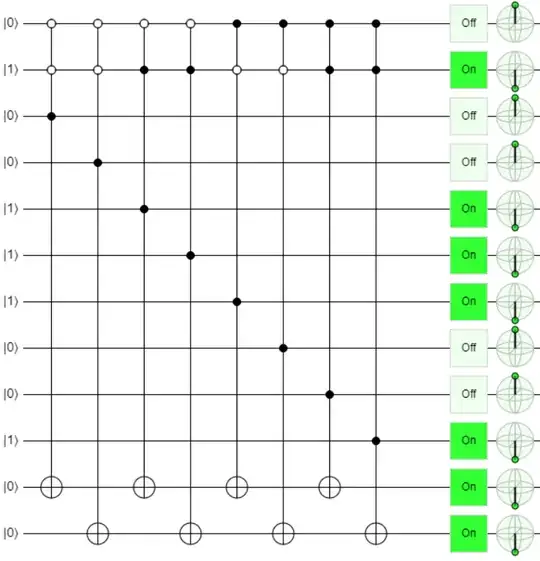
I am trying to create a bit string of |0⟩'s and |1⟩'s in order to create an array.
Would this still break the no-cloning theorem since we do know their state: they are |0⟩'s and |1⟩'s.
If possible, what I am trying to do is that I have the following bit string in 8 qubits:
00011011
and according to another 2 qubits, I would like to 'copy' the 1st 2, the 2nd 2, the 3rd 2 or the 4th 2 qubits to another 2 qubits.
What's the best way to go around this?
Thanks