What is D-Wave's "Pegasus" architecture?

Question

How is D-Wave's Pegasus architecture different from the Chimera architecture?

Answer 1

Pegasus is the first fundamental change in D-Wave's architecture since the D-Wave One.

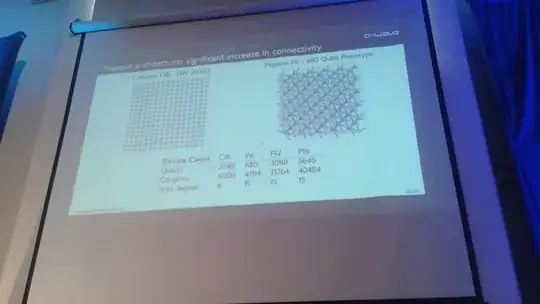
The D-Wave Two, 2X, and 2000Q all used the "Chimera" architecture, which consisted of unit cells of $K_{4,4}$ graphs. The four generations of D-Wave machines just added more qubits by adding more and more unit cells that were the same.

In Pegasus, the actual structure of the unit cells has fundamentally changed for the first time. Instead of the Chimera graph where each qubit can have at most 6 qubits, the Pegasus graph allows each qubit to couple to 15 other qubits.

A machine has been made already with 680 Pegasus qubits (compare this to 2048 Chimera qubits in the D-Wave 2000Q).

The work was presented by Trevor Lanting of D-Wave, four days ago:

Answer 2

Hope this late contribution won't be a meaningless contribution, but as mentioned in one of the comments above, by using D-Waves version of NetworkX you can visualize the Pegasus network. I have attached a few images here of the Pegasus 2 (P2) and Pegasus 6 (P6) architectures using the D-Wave NetworkX.

The reason that I find Pegasus interesting is that the architecture allows for odd number cycles, and of course the obvious scale up in the maximum degree. The theoretical inability for Chimera to have odd cycles is limiting, but practically it can be approximated using minor embedding techniques and maybe imperfect chimera, but of course, Pegasus overcomes that entirely.

Answer 3

How is D-Wave's Pegasus architecture different from the Chimera architecture?

See: "Pegasus: The second connectivity graph for large-scale quantum annealing hardware" (Jan 22 2019), by Nike Dattani (Harvard), Szilard Szalay (Wigner Research Centre), and Nick Chancellor (Durham). Figures were made with their open source software PegasusDraw.

"The 128 qubits of the first commercial quantum annealer (D-Wave One, released in 2011) were connected[by a graph called Chimera (first defined publicly in 2009 [1]), which is rather easy to describe: A 2D array of $K_{4,4}$ graphs, with one ‘side’ of each $K_{4,4}$ being connected to the same corresponding side on the $K_{4,4}$ cells directly above and below it, and the other side being connected to the same corresponding side on the $K_{4,4}$ cells to the right and left of it (see Figure 1). The qubits can couple to up to 6 other qubits, since each qubit couples to 4 qubits within its $K_{4,4}$ unit cell, and to 2 qubits in the $K_{4,4}$ cells above and below it, or to the left and right of it. All commercial quantum annealers built to date follow this graph connectivity, with just larger and larger numbers of $K_{4,4}$ cells (see Table 1). $$\begin{array}{lc} &\text{Array of }K_{4,4}\text{ cells} & \text{Total # of qubits} \\ \text{D-Wave One} & 4 \times 4 & 128 \\ \text{D-Wave Two} & 8 \times 8 & 512 \\ \text{D-Wave 2X} & 12 \times 12 & 1152 \\ \text{D-Wave 2000Q} & 16 \times 16 & 2048 \end{array} $$ $$\text{Table I: Chimera graphs in all commercial quantum annealers to date.}$$

In 2018, D-Wave announced the construction of a (not yet commercial) quantum annealer with a greater connectivity than Chimera offers, and a program (NetworkX) which allows users to generate certain Pegasus graphs. However, no explicit description of the graph connectivity in Pegasus has been published yet, so we have had to apply the process of reverse engineering to determine it, and the following section describes the algorithm we have established for generating Pegasus.

[1] H. Neven, V. S. Denchev, M. Drew-Brook, J. Zhang, W. G. Macready, and G. Rose, NIPS 2009 Demonstration: Binary Classification using Hardware Implementation of Quantum Annealing, Tech. Rep. (2009).

There are a few dozen illustrations in that paper, verified by Kelly Boothby of D-Wave, I don't want to overquote; I believe I've covered the gist of it.

A few points:

• Every qubit is associated with 6 indices: (x, y, z, i, j, k).

• The degree of the vertices (which is 15) has increased by a factor of 2.5 when compared to the degree of Chimera (which is 6), except the cells at the boundary.

• Pegasus' non-planarity expands on the number of binary optimization problems that cannot yet be solved in polynomially time on a D-Wave.

• All quadratization gadgets for single cubic terms which require one auxiliary qubit, can be embedded onto Pegasus with no further auxiliary qubits because Pegasus contains $K_4$, which means that all three logical qubits and the auxiliary qubit can be connected in any way, without any minor-embedding.

See also: "Quadratization in discrete optimization and quantum mechanics", (Jan 14 2019), by Nike Dattani. GitHub source code.