Construct Controlled-$G^{\dagger}$ from known Controlled-$G$

Question

Let there be a known a scheme (quantum circuit) of Controlled-G, where unitary gate G has G$^†$ such that G≠G$^†$ and GG$^†$=I (for example S and S$^†$, T and T$^†$, V and V$^†$, but not Pauli and H gates).

My question for the experts is:

How is correct that new scheme of Controlled-G$^†$ gate may be constructed from this known scheme of Controlled-G gate by reversing the order of used gates (U) and each U in this scheme changes to the corresponding U$^†$ (if U≠U$^†$ of course)?

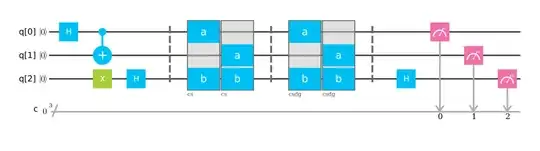
For example, see below my OPENQASM-program (note that suffix 'dg' for gate name is used instead '$^†$'in OPENQASM), where it is used well-known scheme of Controlled-S gate and my scheme of Controlled-S$^†$ gate, constructed from this well-known scheme by the above method.
So far I have only received successful results of applying this method and have not found any obvious contradictions with the known theory ^[*], but suddenly I didn't take something into account.

My program in OPENQASM for example:

//Name of Experiment: Amy Matthew controlled-s and my controlled-sdg gates v7
OPENQASM 2.0; 
include "qelib1.inc";
qreg q[3];
creg c[3];
gate cs a,b {
// a is control, b is target
// see https//uwspace.uwaterloo.ca/bitstream/handle/10012/7818/AmyMatthew.pdf
// fig.4.6b
cx b,a;
tdg a;
cx b,a;
t a;
t b;
}
gate csdg a,b {
// a is control, b is target
// my controlled-sdg (I hope that is reverse of controlled-s)
tdg b;
tdg a;
cx b,a;
t a;
cx b,a;
}

h q[0];
cx q[0],q[1]
;
x q[2];
h q[2];
barrier q;
cs q[0],q[2];
cs q[1],q[2];
barrier q;
csdg q[0],q[2];
csdg q[1]

,q[2];

barrier q;
h q[2];
measure q -> c; 

[*]: Elementary gates for quantum computation Barenco et al. (1995)

Answer 1

How is correct that new scheme of Controlled-$G^\dagger$ gate may be constructed from this known scheme of Controlled-G gate by reversing the order of used gates ($U$) and each $U$ in this scheme changes to the corresponding $U^\dagger$ (if $U≠U^\dagger$ of course)?

It's 100% correct:

Inverting a composed quantum gate is done with the algorithm you gave. You can check for example the implementation of the inverse() method in qiskit.CompositeGate:

def inverse(self):
    """Invert this gate."""
    # self.data is a list of the quantum gates composing the CompositeGate.
    self.data = [gate.inverse() for gate in reversed(self.data)]
    self.inverse_flag = not self.inverse_flag
    return self

Inverting a controlled-gate boils down to apply the controlled-[inverse of this gate].

Answer 2

If I understand the question correctly, you're assuming that you have some gate $V$ that you've decomposed as $\prod_{i=1}^NU_i$ and you want to show that $V^\dagger$ is $\prod_{i=1}^NU_{N+1-i}^\dagger$ where the product is taken in the opposite order?

In that case, you just need to show that $VV^\dagger=\mathbb{I}$ given that $U_iU_i^\dagger=\mathbb{I}$. You can do this directly using the stated decompositions above: $$ VV^\dagger=(U_1U_n\ldots U_N)(U_N^\dagger\ldots U_2^\dagger U_1^\dagger)=U_1U_n\ldots U_{N-1}(U_NU_N^\dagger)U_{N-1}^\dagger\ldots U_2^\dagger U_1^\dagger $$ and so on.

This solution is completely general, and does not need to make any assumptions about the form of the original unitary $V$.