What is wrong with my circuit for the fourth-root of $X$?

Question

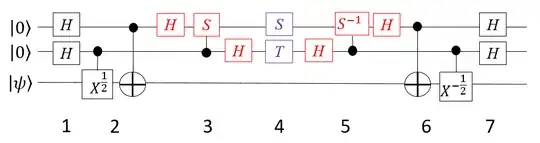
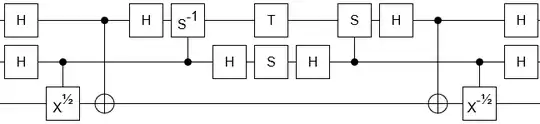
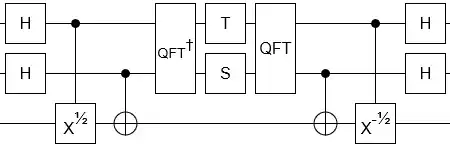
For learning purposes I would like to hand-craft my own circuit for the fourth-root of $X$, using $S$, $T$, and $\sqrt X$ gates.

Note that $\sqrt[4]X$ is of order eight while $\sqrt X$ is of order four, and we can use two ancillas to temporarily store the respective eigenspace. The recipe that I have been following is to:

1. Hit both ancilla with a Hadamard $H$,
2. Have the lower-order ancilla perform a controlled $\sqrt X$ on the target with the higher-order ancilla perform a controlled $X$ on the target,
3. Perform a QFT on the ancillas,
4. Phase the ancillas,
5. Perform an IQFT on the ancillas,
6. Have the higher-order ancilla perform another controlled $X$ while the lower-order ancilla performs a controlled $X^{-1/2}$, and
7. Hit both ancillas with an $H$ to revert:

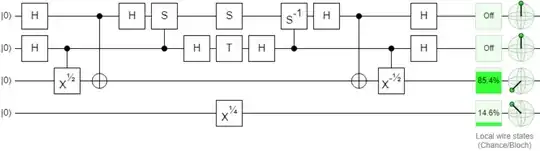
I try the above circuit in Quirk; although the ancillas properly revert $|0\rangle$, it gives me a different answer on the target than Quirk's native $\sqrt[4] X$. On the Bloch sphere my recipe says the target's $\theta$ is $135^\circ$ while the native $\sqrt[4] X$ should be at $45^\circ$.

Did I get my endian-convention wrong on the QFT (red)? Or did I do the uncomputing wrong? Did I not phase properly (purple)?

Here's a Quirk snapshot to compare. The hand-crafted circuit is on the first three qubits with the ancilla the first two qubits and the target the third qubit, while the native $\sqrt[4] X$ for comparison is the fourth qubit. The Bloch spheres/amplitudes are different between the third qubit (my circuit) and Quirk's native circuit:

Answer 1

With the gates you allowed, you can conjugate the $T$ so that it rotates around $X$ instead of $Z$. That gives you $\sqrt[4]X$.

In your circuit I think you got your QFTs backwards, so the phase estimation is estimating the negation of the phase. This is negating the rotation you apply, and making both bits of the phase estimation register relevant instead of just one as should be the case for this case.

Also I think you got your endianness backwards. The S and the T in the center might be in the wrong order. This might be because you didn't include swaps as part of your decomposed QFTs.

An endian error and a sign error. The eternal struggle against mundane mistakes continues. Fixing them both makes it work.

or, using the built-in QFT (and switching some other endian stuff):

Answer 2

I think it's actually far easier than this. You only need one ancilla. The trick is that $X$ has the same eigenvectors as $\sqrt[4]X$. So, you can just do the following

The circuit that you've attempted is for when you've already got a controlled-$U$ for which the eigenvalues of $U$ $\omega$ with $\omega^4=1$. What you're trying to do is construct the effect of such a $U$ starting from a controlled-$V$ where $V^2=I$ so you only need one ancilla (basically, to detect if the bottom qubit is in the $|+\rangle$ state (don't add a phase) or the $|-\rangle$ state (add a phase).