How to inject a $Y^{\frac{1}{4}}$ gate into a circuit

Question

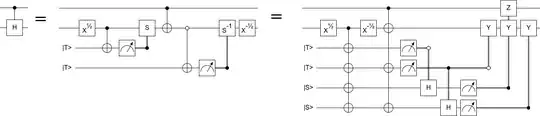
I need to perform a controlled-$H$ gate, which is non-Clifford.

Its standard decomposition is $$Y^{-\frac{1}{4}}_b\cdot CX^{\phantom{\frac{1}{4}}}_{a,b}\cdot Y^{\frac{1}{4}}_b.$$

By means of some auxiliary qubits, one should be able to inject a $Y^{\frac{1}{4}}$ ($Y^{-\frac{1}{4}}$) gate.

What is a possible circuit implementation for this?

Answer 1

You can do $Y^{1/4}$ the same way you do $Z^{1/4}$, by consuming a $|T\rangle$ state.