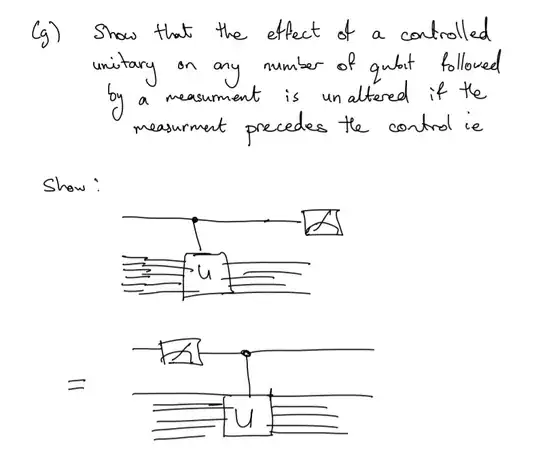
I understand that a Controlled Unitary is just a generalization of a control gate, such as CNOT etc, and that it is given in state representation as $$\hat C_U = |0\rangle\langle0|\otimes\mathbb{I} + |1\rangle\langle1|\otimes \hat U $$or matrix representation of \begin{pmatrix} \mathbb{I} & \textbf{0}\\ \textbf{0} & \textbf{U} \end{pmatrix} The question is asking to show that the time of measurement does not impact the effect of a controlled unitary. I'm unsure how to show this.
Suppose $U$ acts on $n$ qubits and let $|\psi\rangle$ be an arbitrary normalized state of $n+1$ qubits
$$ |\psi\rangle=|0\rangle|\psi_0\rangle+|1\rangle|\psi_1\rangle\tag1 $$
where $|\psi_0\rangle$ and $|\psi_1\rangle$ are not necessarily normalized states of $n$ qubits.
Consider first the situation where we begin by applying controlled-$U$. After the controlled-$U$ the $n+1$ qubits are in state
$$ CU|\psi\rangle = |0\rangle|\psi_0\rangle+|1\rangle U|\psi_1\rangle.\tag2 $$
Let $P_0=|0\rangle\langle 0|$ and $P_1=|1\rangle\langle 1|$. If measurement yields $0$, the unnormalized post-measurement state is
$$ (P_0\otimes I_n)CU|\psi\rangle = P_0|0\rangle|\psi_0\rangle+P_0|1\rangle U|\psi_1\rangle = |0\rangle|\psi_0\rangle\tag3 $$
where $I_n$ denotes the identity on the last $n$ qubits. Similarly, if measurement yields $1$, the unnormalized post-measurement state is
$$ (P_1\otimes I_n)CU|\psi\rangle = P_1|0\rangle|\psi_0\rangle+P_1|1\rangle U|\psi_1\rangle = |1\rangle U|\psi_1\rangle.\tag4 $$
Consider now the situation where we begin by measuring the first qubit. If measurement yields $0$, the unnormalized post-measurement state is
$$ P_0|\psi\rangle = P_0|0\rangle|\psi_0\rangle+P_0|1\rangle|\psi_1\rangle = |0\rangle|\psi_0\rangle\tag5 $$
and if it yields $1$, the unnormalized post-measurement state is
$$ P_1|\psi\rangle = P_1|0\rangle|\psi_0\rangle+P_1|1\rangle|\psi_1\rangle = |1\rangle|\psi_1\rangle.\tag6 $$
Applying classically controlled $U$ to the last $n$ qubits when measurement result is $1$ we get
$$ (I_1\otimes U)|1\rangle|\psi_1\rangle=|1\rangle U|\psi_1\rangle.\tag7 $$
Comparing $(3)$ with $(5)$ and $(4)$ with $(7)$ we see that the unnormalized post-measurement state is the same in both scenarios regardless of measurement result. Since measurement outcome probability is the squared norm of the unnormalized post-measurement state we see that both measurement outcomes have the same probability in each scenario. Finally, equality of the unnormalized post-measurement states implies equality of the normalized post-measurement states. Thus, measurement outcome probabilities and the post-measurement states of all $n+1$ qubits are the same in the two scenarios.
The above reasoning can be compressed by noting that
$$ CU = P_0\otimes I_n + P_1\otimes U. $$
This way of writing down controlled-$U$ makes it clear that
$$ (P_i\otimes I_n) \circ CU = CU \circ (P_i\otimes I_n) $$
for $i=0,1$ which means that controlled gates and computational basis measurements on the control qubit commute.