What is the mathematical intuition behind deferred measurement?

Question

Please give a complete proof of the principle of Deferred Measurement Principle, including careful notation (preferably explaining the meaning of each symbol) and rigorous mathematical reasoning (preferably giving the rationale or references for each step of the derivation).

Answer 1

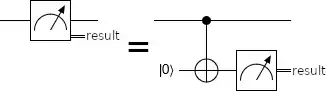
For me the intuition is the 'ancillary measurement principle'. Measuring with an ancilla is the same as inline measurement:

You can then easily see it's possible to move the CNOT from before the measurement to after the measurement, as long as you know CNOTs commute when they only touch at the control:

Now you might say this is not a proof, because at the end the control is on the output qubit instead of the output bit. And that's right. But you didn't ask for a proof you asked for the intuition.

My intuition is it's much clearer that the qubit has the same value as the bit after the measurement. Because at that point the qubit has been collapsed into the computational basis. So the deferred measurement principle becomes blatantly obvious, and it's just a matter of grinding the algebra to see it's actually equivalent.