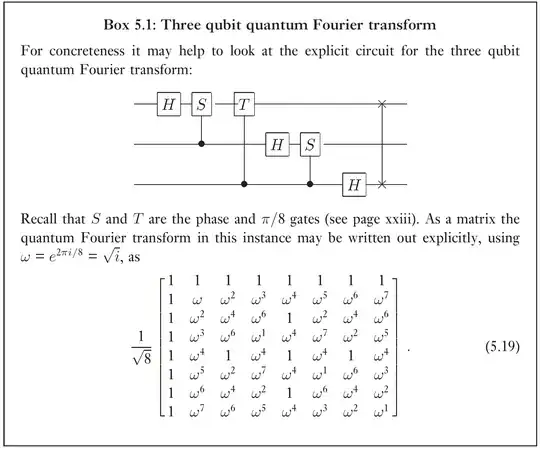
I am currently going through Nielsen's QC bible and having still some foundational / conceptual problems with the matter.
I have tried to retrieve this $8 {\times} 8$ matrix describing the QFT of 3 qubits via Kronecker product in various attempts.
Hadamard transform can be decomposed into $H \otimes 1 \otimes 1$, and the others are fundamentally kronecker products of the 4x4 matrices of S resp. T with the 2x2 identity.
Whats wrong with my approach?
EDIT:
$T\text{=}\left( \begin{array}{cccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & e^{\frac{\pi i}{4}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & e^{\frac{\pi i}{4}} \\ \end{array} \right)$
which is derived from $R_k = \left( \begin{array}{cc} 1 & 0 \\ 0 & e^{2 i \pi /2^k} \\ \end{array} \right)$, being $S$ for $k=1$ and $T$ for $k=2$.
EDIT 2:
The controlled T-operation can be represented in computational basis as
$\left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & e^{2 \pi i / 2^k } \\ \end{array} \right)$.
EDIT 3:
In mathematica, one faulty calculation of mine is:
$\text{SWAP}\text{=}\left( \begin{array}{cccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} \right)$
SWAP*KroneckerProduct[IdentityMatrix[2], IdentityMatrix[2], H]KroneckerProduct[IdentityMatrix[2], S] KroneckerProduct[ IdentityMatrix[2], H, IdentityMatrix[2]] * T KroneckerProduct[S, IdentityMatrix[2]] KroneckerProduct[H, IdentityMatrix[2], IdentityMatrix[2]] // MatrixForm
which gives:
$\left( \begin{array}{cccccccc} \frac{1}{2 \sqrt{2}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & -\frac{1}{2 \sqrt{2}} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{e^{\frac{i \pi }{2}}}{2 \sqrt{2}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & -\frac{e^{\frac{i \pi }{2}} i^2}{2 \sqrt{2}} \\ \end{array} \right)$