Understanding Constant Multiplication Circuit for Binary Field - How to Construct Quantum Circuit from Linear Mapping

Question

I was thinking to ask this on Math Stackexchange, but maybe here would be better since I also hope the answers also explain from quantum computation context.

Problem

So I was reading the paper "Concrete quantum-cryptanalysis of binary elliptic curves", and I got stuck in understanding how to construct a multiplication by constant circuit for binary field. In their CHES presentation and their other paper, the authors describe that it is easy to construct the circuit from a matrix since multiplication by constant is just a linear mapping.

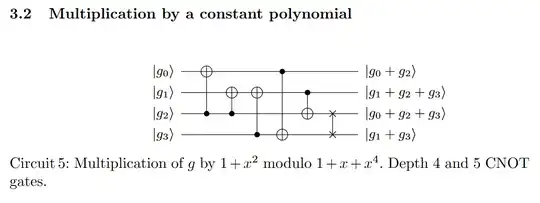
On their other paper, they present this matrix as a representation of multiplication by $1 + x^2$ modulo $1 + x + x^4$:

$\Gamma = \begin{bmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 \end{bmatrix} $

which by LUP decomposition, corresponds to this circuit:

Questions

The questions are interrelated. They are:

1. How to construct matrix $\Gamma$?

2. Why the multiplication matrix is a 4x4 matrix for a 4-qubit circuit? I thought it would be 16x16 $(2^n = 16)$?

3. Is that particular matrix ($\Gamma$) really correct for all values?

My Attempts So Far

For Question 1

My guess is by creating two matrices, e.g., $INPUT$ and $OUTPUT$, which includes all possible inputs and the corresponding output after the constant multiplication. Then, the matrix $\Gamma$ can be obtained from $OUTPUT * INPUT^{-1}$.

I have tried from scratch: calculated all the possible 16 input and the corresponding output pairs (derived from SageMath) and make the mapping (i.e., $\left| x0,x,x^2,x^3 \right> = \left| 0010 \right> \rightarrow \left| 1110 \right>, \left| 0100 \right> \rightarrow \left| 0101 \right>$, and so on...

However, then I realized that the resulting matrix is a rectangular 16x4 matrix rather than a square matrix for each $INPUT$ and $OUTPUT$, so the inversion can not be done when I tried that on Matlab.

For Question 3

For each possible input, I applied $\Gamma$ to verify the output result. While 6 of them are correct, the other 10 are wrong. For example, $\left| 1011 \right> \rightarrow \left| 2231 \right>$ rather than $\left| 0011 \right> $.

I am not sure that kind of paper would contain such errors. So my bet is my approach was all wrong.

I would be very grateful if anyone could guide me on this. Any help is appreciated. Thanks!

Answer 1

Let me start with some background information on this problem as not all people might be familiar with it.

It is well known that finite fields for prime order $p$ can be constructed by taking integers modulo $p$, this is $\mathbb F_p \simeq \mathbb Z / p\mathbb Z$. From this, we can construct certain field extensions, namely Galois extensions, as follows. Consider the univariate polynomial ring $\mathbb F_p[\theta]$ (I don't use $x$ as variable symbol to keep notation clean.) Let $f\in\mathbb F_p[\theta]$ be an irreducible polynomial of degree $m$, this is $f$ cannot be written as a product of two non-constant polynomials. Then, the quotient w.r.t. to the ideal generated by $f$, $\mathbb F_{p^m}:=\mathbb F_p[\theta]/(f)$ is a finite field with $q=p^m$ elements. Its elements can be seen as polynomials in $\theta$ modulo $f$.

Question 1 The first problem you're considering is to find a matrix representation of the multiplication with an element $a = 1+\theta^2$ from the finite field $\mathbb F_{2^4}=\mathbb F_{16}$ (as $1+\theta+\theta^4$ is irreducible). More generally, the additive group of $\mathbb F_{p^m}$ has the structure of a vector space over $\mathbb F_p$, $\mathbb F_{p^m}^+ \simeq \mathbb F_p^m$. Choosing a polynomial basis, i.e. writing any element $b\in\mathbb F_{p^m}$ uniquely as $$ b = b_0 \theta^0 + b_1 \theta^1 + \dots + b_{m-1} \theta^{m-1}, \quad b_i \in \mathbb F_p, $$ induces such an isomorphism by $b \mapsto (b_0,\dots,b_{m-1})\in\mathbb F_p^m$.

Since the multiplication $M_a: b \mapsto ab$ is $\mathbb F_p$-linear, $M_a$ induces a linear map on $\mathbb F_p^m$ which can be written in a basis as a $m\times m$ matrix with coefficients in $\mathbb F_p$.

Now back to your example. To find the matrix representing $M_{1+\theta^2}$ in the standard polynomial basis, we have to act with $1+\theta^2$ on all four basis elements, i.e. on $\theta^0,\dots,\theta^3$. This yields: $$ 1 \mapsto 1+\theta^2, \quad \theta \mapsto \theta + \theta^3, \\ \theta^2 \mapsto \theta^2 + \theta^4 = 1 + \theta + \theta^2, \quad \theta^3 \mapsto \theta(\theta^2+\theta^4) = \theta+\theta^2+\theta^3. $$ We can now extract the expansion coefficients from the images and write them as columns of the matrix representation $$ M_{1+\theta^2} \simeq \begin{pmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 \end{pmatrix} =\Gamma. $$ This should answer Question 3 (btw in your example, you have to take the result modulo 2, since we're in $\mathbb F_2$!).

Question 2 That $M_a$ is a $4\times 4$ matrix should be clear by now. How is this now related to quantum circuits? We can label the computational basis of a $n$-qubit system by vectors $x\in\mathbb F_2^n$, namely we set $$ | x \rangle := | x_1 \rangle \otimes \dots \otimes |x_n\rangle. $$ Matrices $M\in\mathrm{GL}_n(\mathbb F_2)$ act naturally on this basis by $| x \rangle \mapsto | Mx\rangle$, i.e. they only permute the computational basis. As such, they clearly define a unitary $U_M$. Note that the unitary has dimension $2^n \times 2^n$ and complex (here: real) entries but $M$ is a $n\times n$ matrix with binary entries.

Remark: It is a well-known fact that $\mathrm{GL}_n(\mathbb F_2)$, i.e. the reversible linear Boolean circuits, is generated by $CNOT$ gates with representation $$ CNOT_{12} \simeq \begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix}, \quad CNOT_{21} \simeq \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}. $$ This basically follows from the PLU decomposition together with rewritting permutations as CNOT circuits.